# Deep learning
# NN
# 向量化
[1] 神经网络层,a [1] 神经网络第一层,a [0] 神经网络输入层
a^{[1]}_1$$第一层第一个节点 input layer hidden layer:training set中中间数值不可见 output kayer 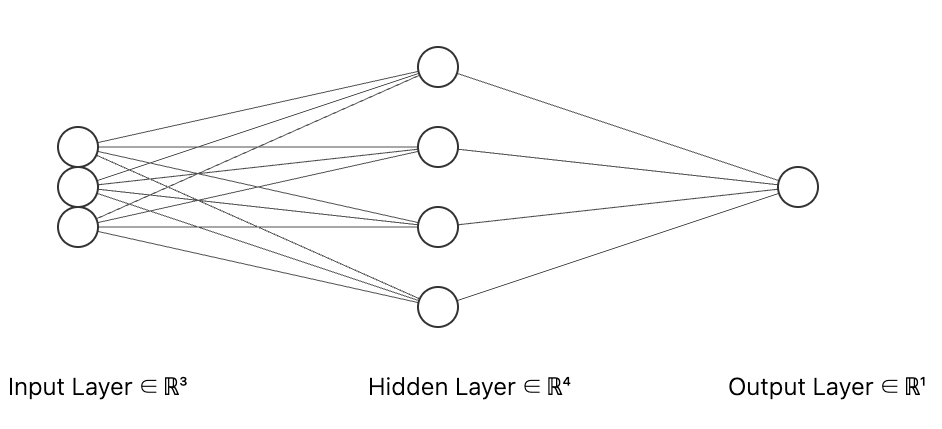 上图有两层,一般不算输入层。双层神经网络 $$ Z_{1}^{[1]} = W_{1}^{[1]T}x + b_{1}^{[1]}, \quad a_{1}^{[1]} = \sigma(Z_{1}^{[1]})\\ Z_{2}^{[1]} = W_{2}^{[1]T}x + b_{2}^{[1]}, \quad a_{2}^{[1]} = \sigma(Z_{2}^{[1]})\\ Z_{3}^{[1]} = W_{3}^{[1]T}x + b_{3}^{[1]}, \quad a_{3}^{[1]} = \sigma(Z_{3}^{[1]})\\ Z_{4}^{[1]} = W_{4}^{[1]T}x + b_{4}^{[1]}, \quad a_{4}^{[1]} = \sigma(Z_{4}^{[1]})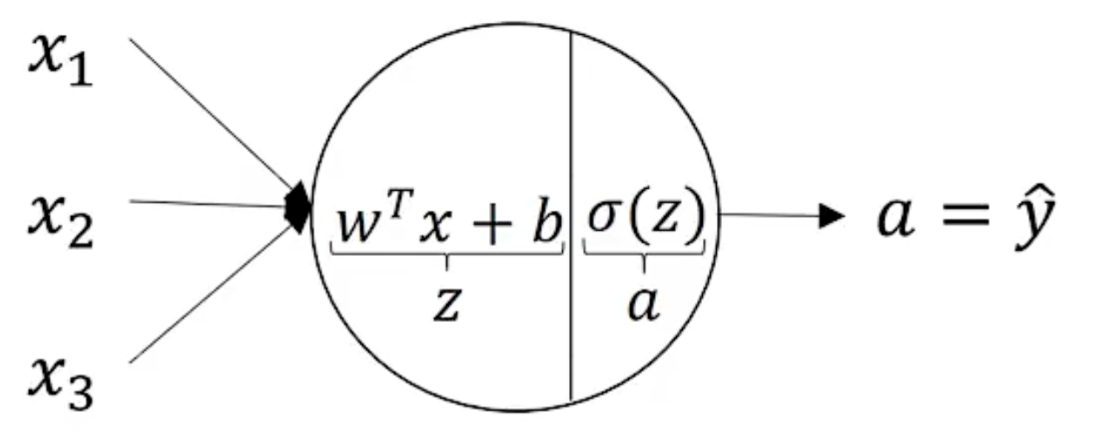
具有多个输入时,$$a^[2](i)}$$,$$z$$
# 激活函数
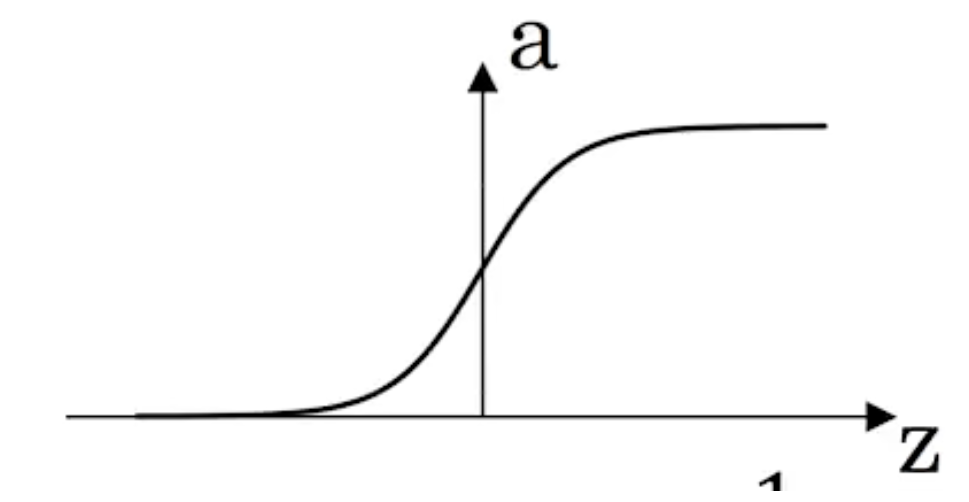
sigmoid $$a=\frac1}{1+e}$$
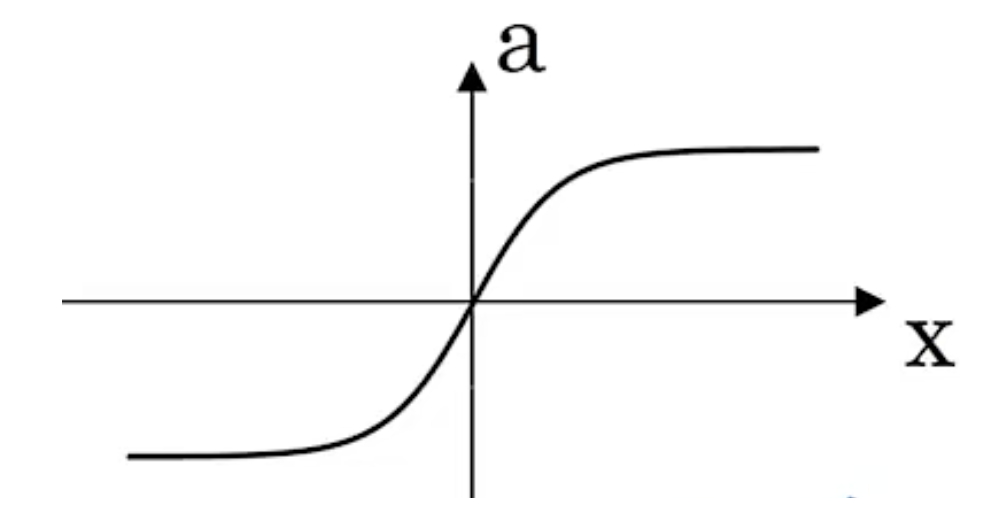
a= tanh(z)=$$\frace}e}$$ 比 sigmoid 激活函数更优越
Relu=max(0,z)
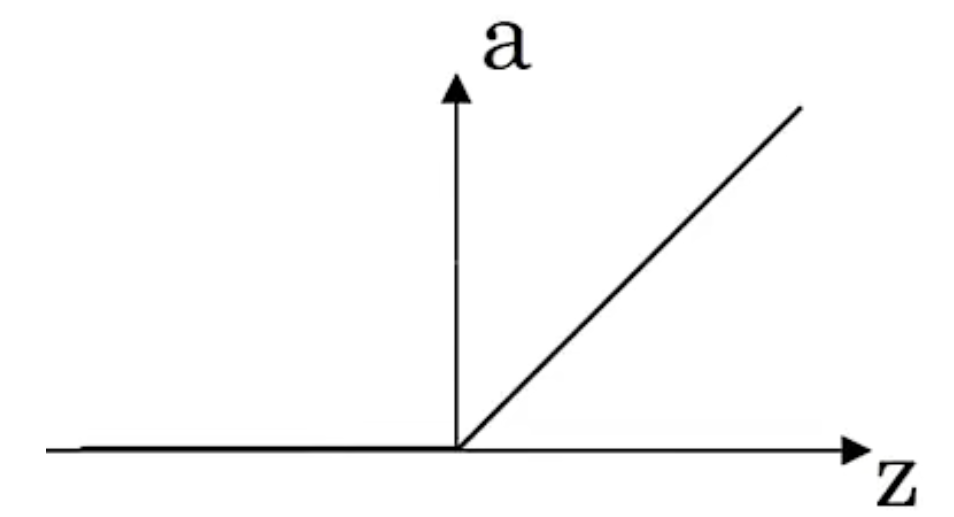
leaky relu**=max(0.01z,z)**
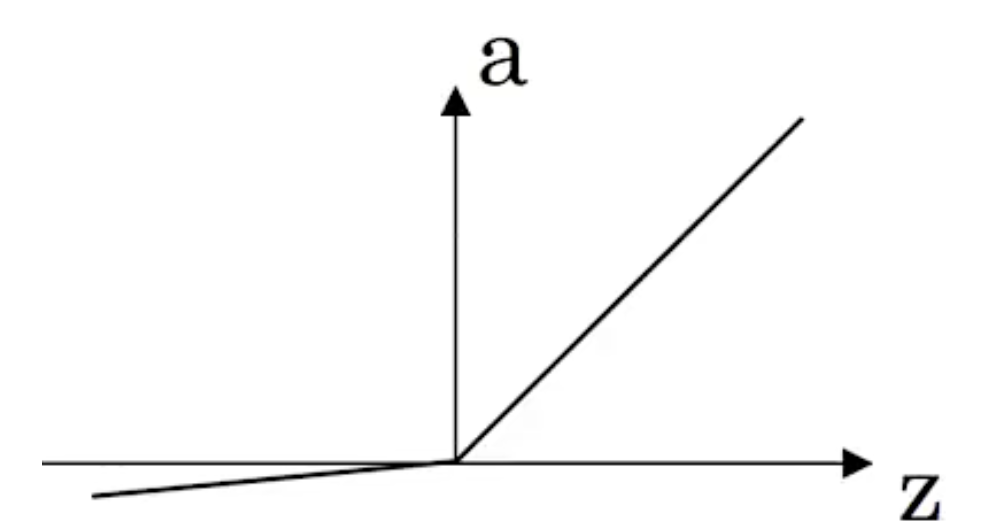
线性激活函数:可以视为没有用激活函数
不同层可以使用不同的激活函数
二分时,输出使用 sigmoid,其他使用 ReLU
使用 relu,学习的更快
对于神经网络,如果使用线性激活或者没有激活,那么使用隐藏层没有意义
只有回归问题,可以在输出层使用线性激活。
# 梯度下降
ReLU’=1/0
leaky relu’=0.01/1
# DNN
n^{[1]}$$第一层的节点数 $$a^{[l]}$$第l层的激活函数 $$w^{[l]}$$$$z^{[l]}$$的权重 $$Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]}
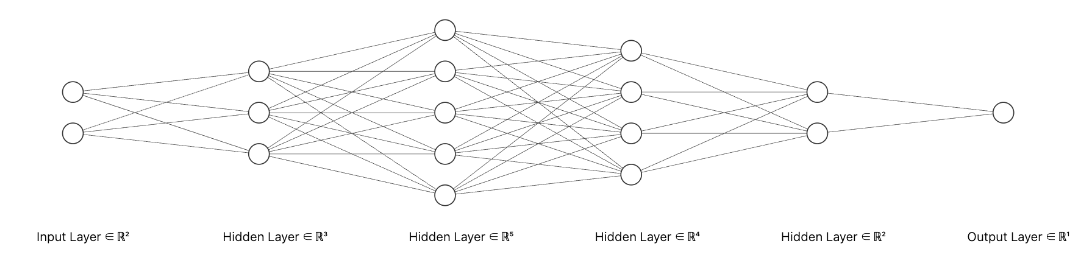
向量化后
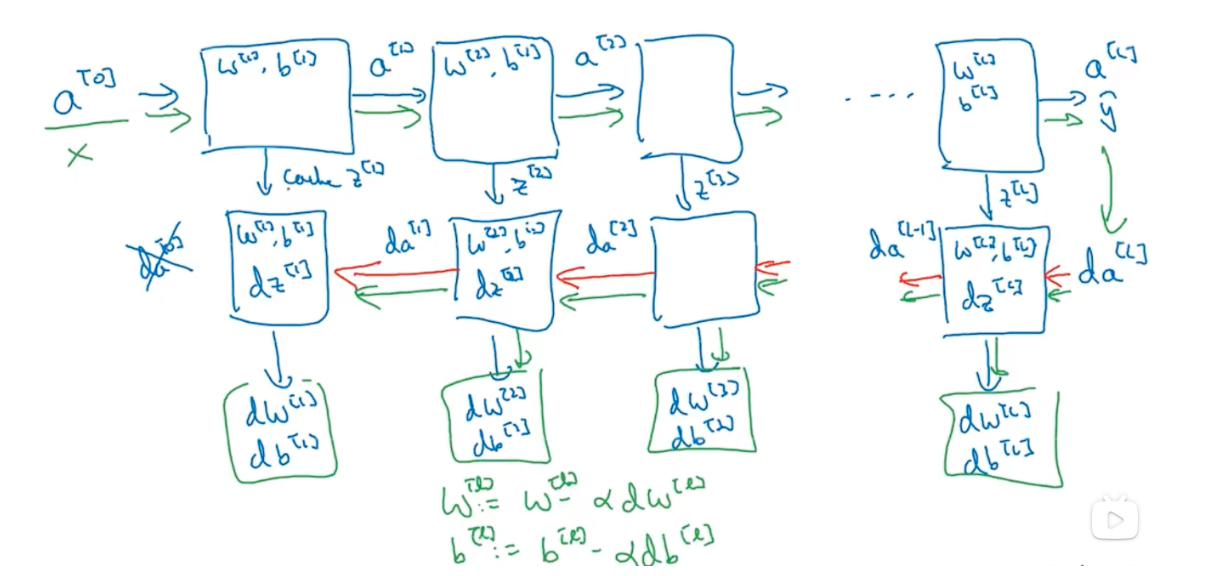
# 超参数
参数
超参数 $$ 学习率:\alpha,$$
hidden layer $$ $$l n^{[l]}$$hidden unit 迭代次数 activation_func,会对w,b造成影响 mometum,minibatch size,regularation parameter 尝试不同的超参数,找到cost最低的参数 ### train/cross/test set 70-30 train-test 60-20-20 train-cross-test 数据量变大后,不再需要那么多cross set和test set 确保dev set和test set 来自同一分布 没有test set也没关系,有dev set 也行 ### bias-variance high bias - underfitting - train set和dev set表现都不好 - bigger network/train longer/nn architecture search high variance - overfitting - train set表现好,dev set表现不好。- more data/regularation/nn architecture search | train set error | 1% | 15% | 15% | 0.5% | | --------------- | -------------- | --------- | ------------------------ | ---------------------- | | dev set error | 11% | 16% | 30% | 1% | | | high variance | high bias | high bias &high variance | low bias &low variance | ### regularation logistic regression中,J(w)中添加 $$\frac{\lambda}{2m} \begin{Vmatrix} w \end{Vmatrix}_2^2$$,$$\lambda$$是正则化参数 $$\begin{Vmatrix} w \end{Vmatrix}_2^2=\sum_{j=1}^{n_x}w_j^{2}=w^Tw$$,称为L2正则化 $$\begin{Vmatrix} w \end{Vmatrix}_1=\sum_{j=1}^{n_x}\begin{vmatrix} w_j \end{vmatrix}$$,最终w是稀疏的,即w中有很多0,称为L1正则化 nn中$$J(w ^{[1]},b^{[1]}...)=\frac{1}{m}\sum_{i=1}^{m}L(\hat{y}^{i},y^{i})+\frac{l}{2m}\sum_{l=1}^{L}\begin{Vmatrix} w^{[l]} \end{Vmatrix}^2_F \begin{Vmatrix} w^{[l]} \end{Vmatrix}^2_F=\sum_{i=1}^{n^{[l-1]}}\sum_{j=1}^{n^{[l]}}(w_{ij}^{[l]})^2$$,w$$(n^{[l-1]},n^{l}) \lambda$$ 增大,$$w^{[l]} 减小$$,$$z^{[l]}$$取值范围变小,tanh场景,接近线性,线性可以减少过拟合 ### dropout正则化 keep-prob 保留隐藏单元的概率,对于可能过拟合的层,可以设置较低的参数。每层prob参数可以是不同的 随机剔除单元,实现正则化 一般在计算机视觉中应用比较多。使用dropout后,J不再明确 ### 其他正则化 通过假样本扩充数据集。比如扭曲,翻转等 提前停止、 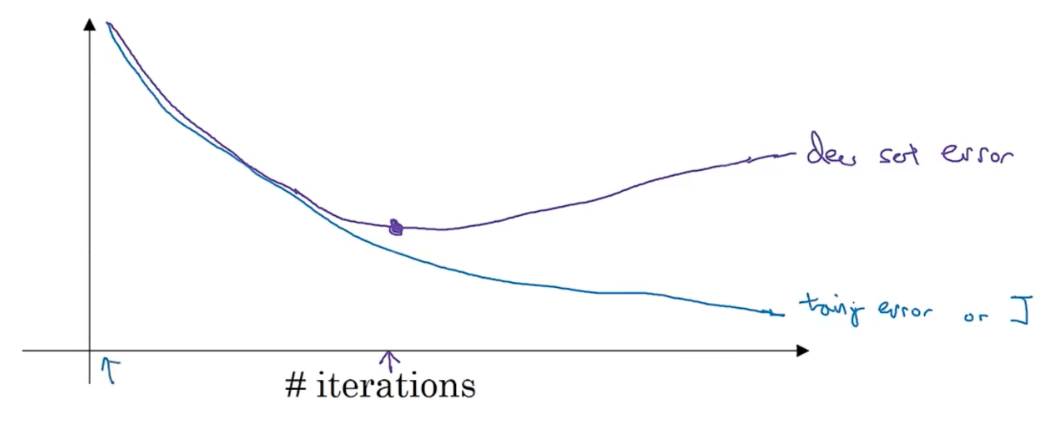 ### 归一化 $$\mu=\frac{1}{m}\sum_{i=1}^{m}x^{(i)}$$,$$x:=x-\mu
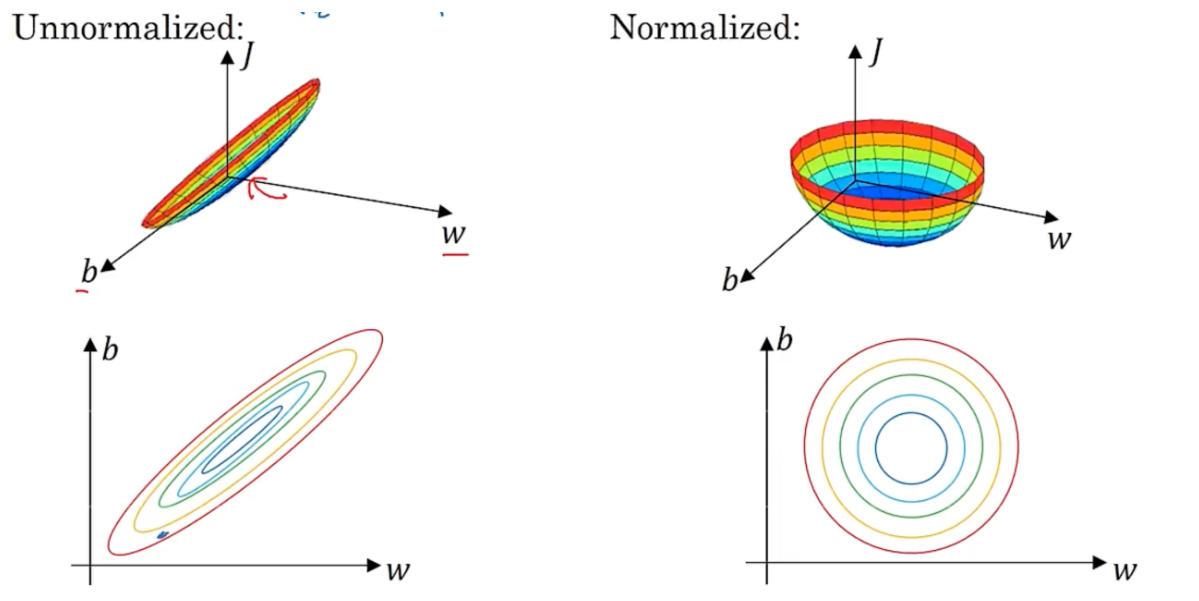
未归一化会使梯度下降时变得震荡
# 梯度消失 梯度爆炸
随机权重初始化解决
relu:
tanh
# mini batch
把大 train set 拆分成若干个小 train set
mini batch 梯度下降
每次计算 mini batch 个 cost ,而不是一整个 batch。即对于 $$xt,yt $$
一个周期内可以进行更多次的梯度下降,下降的会更快
# 指数加权平均
vt $$= \frac{1}{1-\beta}$$ days average temp
# momentum
在第 t 轮迭代,计算 dw,db,在当前的 mini batch
使垂直方向振动变小,快速水平移动。抑制路径中的震荡
常见的 $$\beta$$ 是 0.9
# RMSprop
在第 t 轮迭代,计算 dw,db,在当前的 mini batch
减缓垂直方向更新
垂直方向除以更大的的数 $$\sqrt {sdb}$$ 抑制震荡
水平方向除以更小的数,增大水平移动
# Adam
在第 t 轮迭代,计算 dw,db,在当前的 mini batch
\beta_1$$ 默认0.9 $$\beta_2$$推荐0.999 $$\epsilon$$推荐 10^(-8) ### 降低学习率 学习接近收敛时,降低学习率 学习率衰减 $$\alpha=\frac{1}{1+decay\_rate*epoch\_num}*\alpha_0
指数衰减
\alpha=\frac{k}{\sqrt{epoch\_num}}*\alpha_0$$,k是常数 ### 调整超参数 $$\alpha > \beta\&mini\_batch\_size\&hidden\_unit > layers\&learning\_rate\_decray > \epsilon\&\beta_1\&\beta_2
随机采样
非网格搜索
粗细采样
定期确认学习率
只对一个模型进行精细学习率调整 /// 同步训练很多模型 取决于有多少计算资源
# batch-normalization
归一化 $$z {[i]}$$, 会是训练 $$w^{[i+1]},b$$ 更快
x->z^{[1]}$$ 参数w1,b1 $$z^{[1]}->\tilde{z}^{[1]}$$ 参数$$\beta^{[1]},\gamma^{[1]}
可以对于 mini batch 运用 batch-norm
可以去除 b,在 batch-nom 中
# softmax
损失函数
backprop:$$d_z^{[l]}=\hat{y}-y$$
# TL
A-> B
TASK A,B 有相同输入
A 的数据远多于 B
A 的底层特征对 B 有用
多任务学习
# CNN
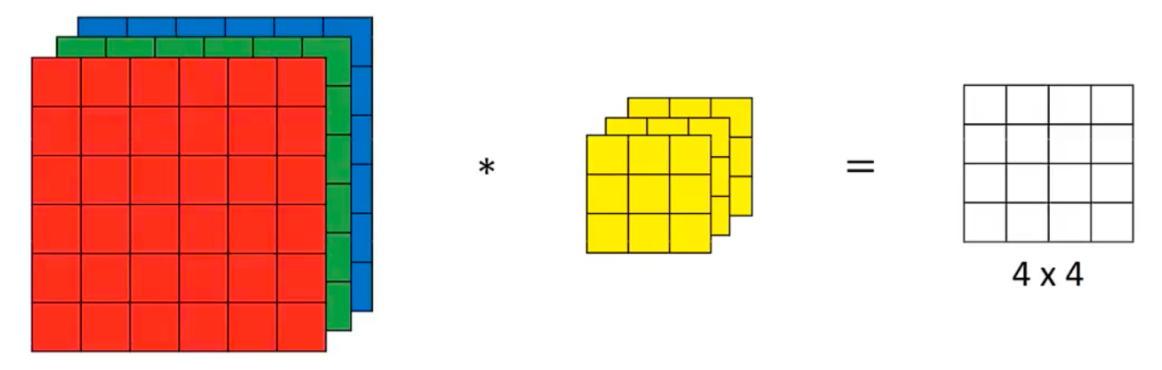
# 卷积运算
卷积是数学分析中的一种积分变换的方法,在图像处理中采用的是卷积的离散形式。这里需要说明的是,在卷积神经网络中,卷积层的实现方式实际上是数学中定义的互相关(cross-correlation)运算。
卷积核(kernel)也被叫做滤波器(filter),假设卷积核的高和宽分别为𝑘ℎ和𝑘𝑤,则将称为𝑘ℎ×𝑘𝑤卷积,比如 3×5 卷积,就是指卷积核的高为 3, 宽为 5。
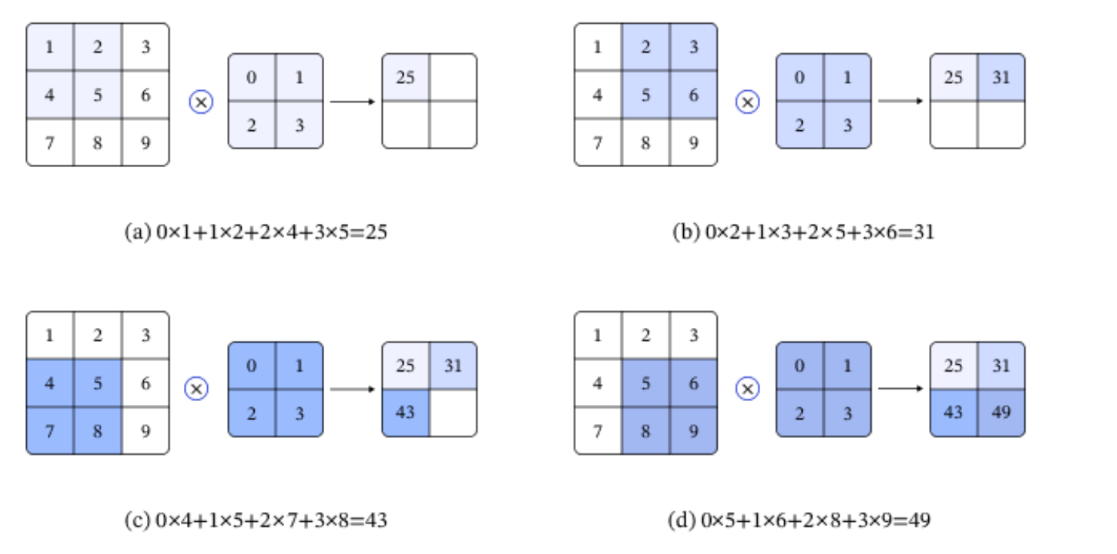
在卷积神经网络中,一个卷积算子除了上面描述的卷积过程之外,还包括加上偏置项 (引入非线性运算、增强模型拟合能力) 的操作。例如假设偏置为 1,则上面卷积计算的结果为:
[26,32,44,50]
# 垂直边缘检测
卷积核 /filter,下面 3*3 矩阵为卷积核
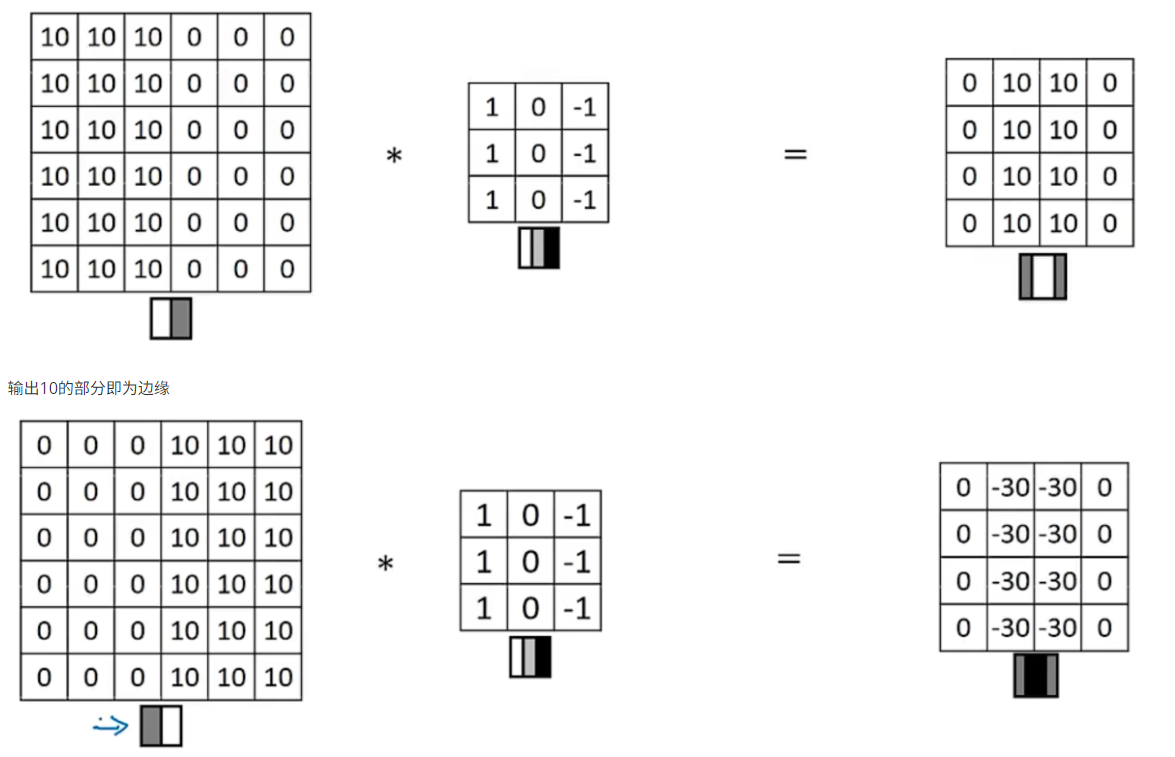
几种不同的 filter
| 1 | 0 | -1 |
|---|---|---|
| 2 | 0 | -2 |
| 1 | 0 | -1 |
sobel filter
| 3 | 0 | -3 |
|---|---|---|
| 10 | 0 | -10 |
| 3 | 0 | -3 |
shar filter
filter 中所有参数可以通过反向传播学习到,不再只是垂直或水平检测边缘
# padding
如果输入尺寸为 4,卷积核大小为 3 时,输出尺寸为 4−3+1=2。读者可以自行检查当输入图片和卷积核为其他尺寸时,上述计算式是否成立。当卷积核尺寸大于 1 时,输出特征图的尺寸会小于输入图片尺寸。如果经过多次卷积,输出图片尺寸会不断减小,边界和角落像素丢失越来越多,导致模型训练效果不佳。且当卷积核的高度和宽度不同,通过填充 (padding) 使输入和输出具有相同的宽和高。
nn 的输入,ff 的 filter,最终输出 (n-f+1,n-f+1)
在周围填充一圈 0,(n+2p-f+1 , n+2p-f+1),保持了原始大小
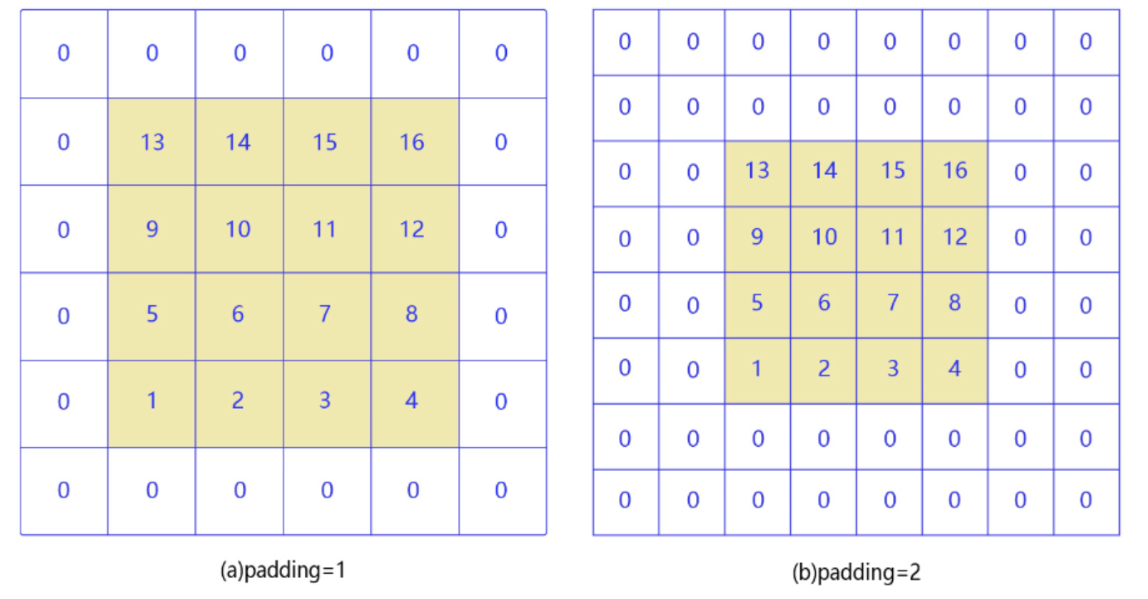
vaild 卷积代表无填充 (n-f+1,n-f+1)
same 卷积:输出和输入大小一样(n+2p-f+1)*(n+2p-f+1),p=(f-1)/2
卷积核大小通常使用 1,3,5,7 这样的奇数,如果使用的填充大小为𝑝ℎ=(𝑘ℎ−1)/2,𝑝𝑤=(𝑘𝑤−1)/2,则卷积之后图像尺寸不变。例如当卷积核大小为 3 时,padding 大小为 1,卷积之后图像尺寸不变;同理,如果卷积核大小为 5,padding 大小为 2,也能保持图像尺寸不变。
# 卷积步长 - stride
卷积核每次滑动一个像素点,这是步幅为 1 的特殊情况。步幅为 2 的卷积过程,卷积核在图片上移动时,每次移动大小为 2 个像素点。
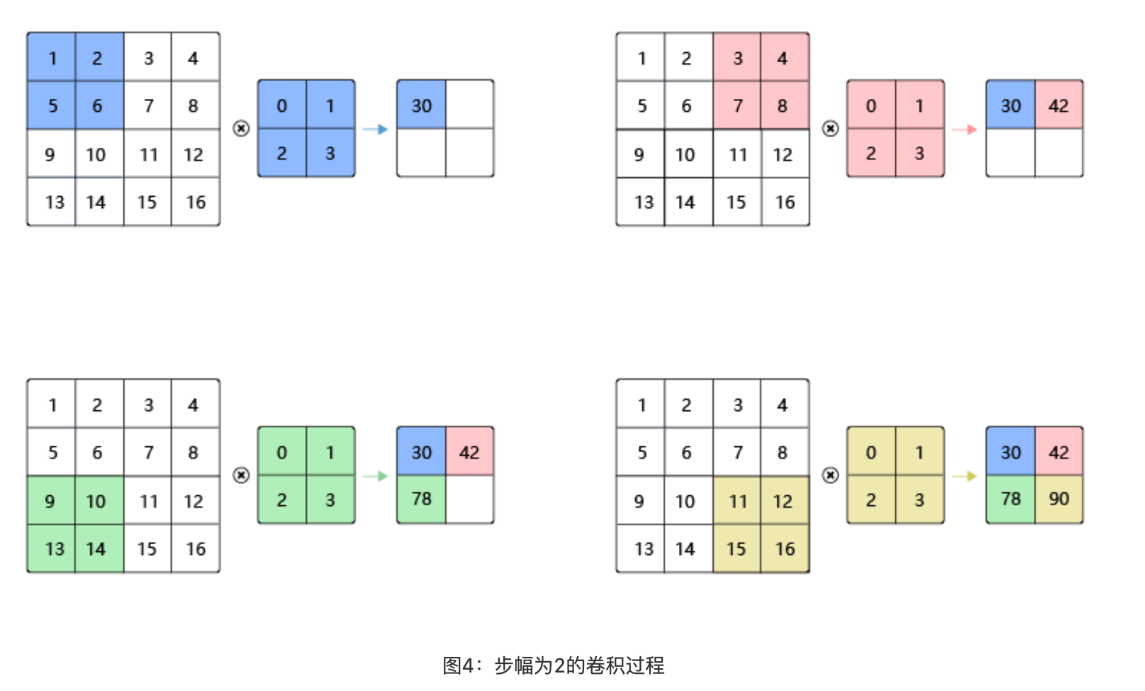
步长为 s 的时候,输出大小是 $$(\frac {n+2p-f}{2}+1,\frac {n+2p-f}{2}+1)$$
如果不是整数,向下取整。即如果 filter 不完全在输入中,就不计算
一般不对 filter 进行镜像。卷积满足结合率
# 感受野
输出特征图上每个点的数值,是由输入图片上大小为𝑘ℎ×𝑘𝑤的区域的元素与卷积核每个元素相乘再相加得到的,所以输入图像上𝑘ℎ×𝑘𝑤区域内每个元素数值的改变,都会影响输出点的像素值。我们将这个区域叫做输出特征图上对应点的感受野。感受野内每个元素数值的变动,都会影响输出点的数值变化。比如 3×3 卷积对应的感受野大小就是 3×3
当通过两层 3×3 的卷积之后,感受野的大小将会增加到 5×5。当增加卷积网络深度的同时,感受野将会增大,输出特征图中的一个像素点将会包含更多的图像语义信息。
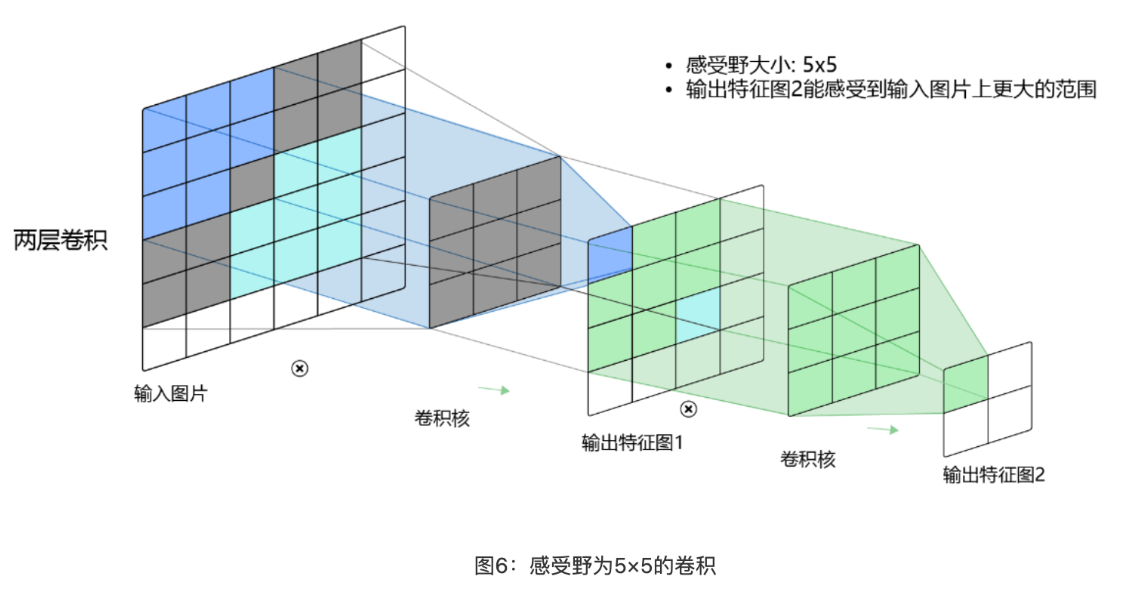
# 多维卷积
对于彩色图片有 RGB 三个通道,需要处理多输入通道的场景。输出特征图往往也会具有多个通道,而且在神经网络的计算中常常是把一个批次的样本放在一起计算,所以卷积算子需要具有批量处理多输入和多输出通道数据的功能。
hightweightchannel
输入 channel 和 filter channel 必须相同
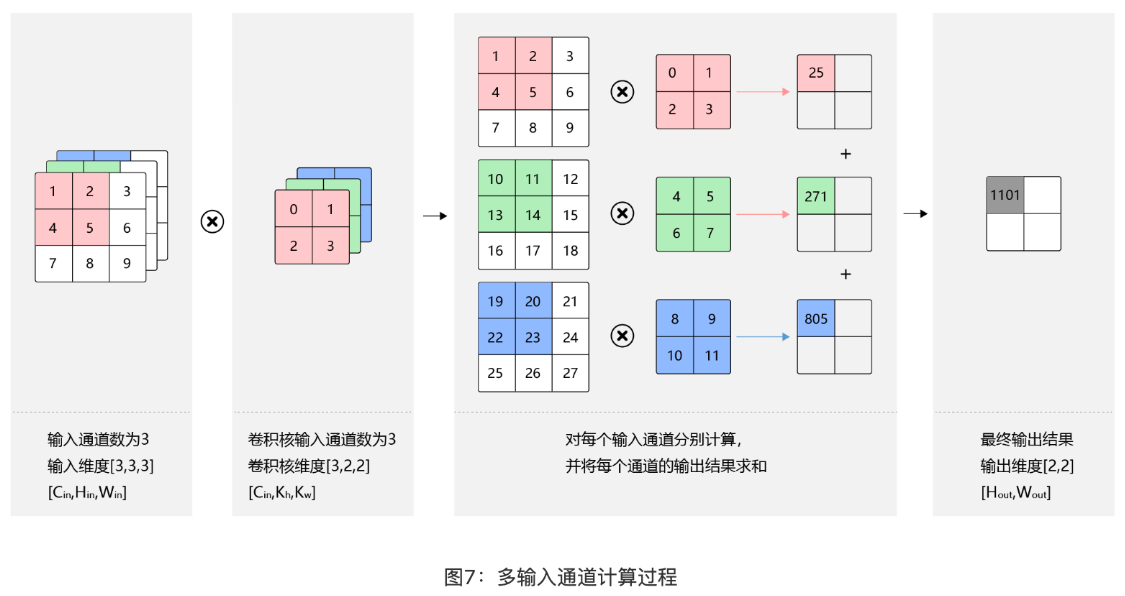
多 channel filter 维度计算
n 输入,f 是 filter,nc 是 channel
(n*n*n_c , f*f*n_c) ->(n-f+1,n-f+1,nc^{'})$$,$$nc^{'}取决于有多少个filter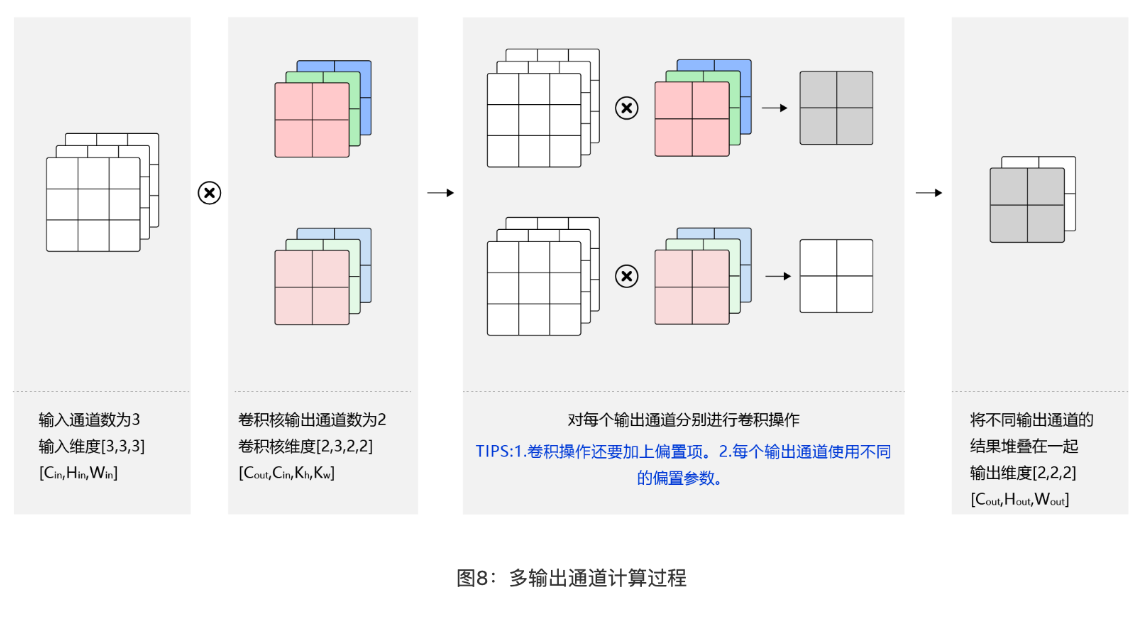
# batch
在卷积神经网络的计算中,通常将多个样本放在一起形成一个 mini-batch 进行批量操作,即输入数据的维度是𝑁×𝐶𝑖𝑛×𝐻𝑖𝑛×𝑊𝑖𝑛。由于会对每张图片使用同样的卷积核进行卷积操作,卷积核的维度与上面多输出通道的情况一样,仍然是𝐶𝑜𝑢𝑡×𝐶𝑖𝑛×𝑘ℎ×𝑘𝑤,输出特征图的维度是𝑁×𝐶𝑜𝑢𝑡×𝐻𝑜𝑢𝑡×𝑊𝑜𝑢𝑡
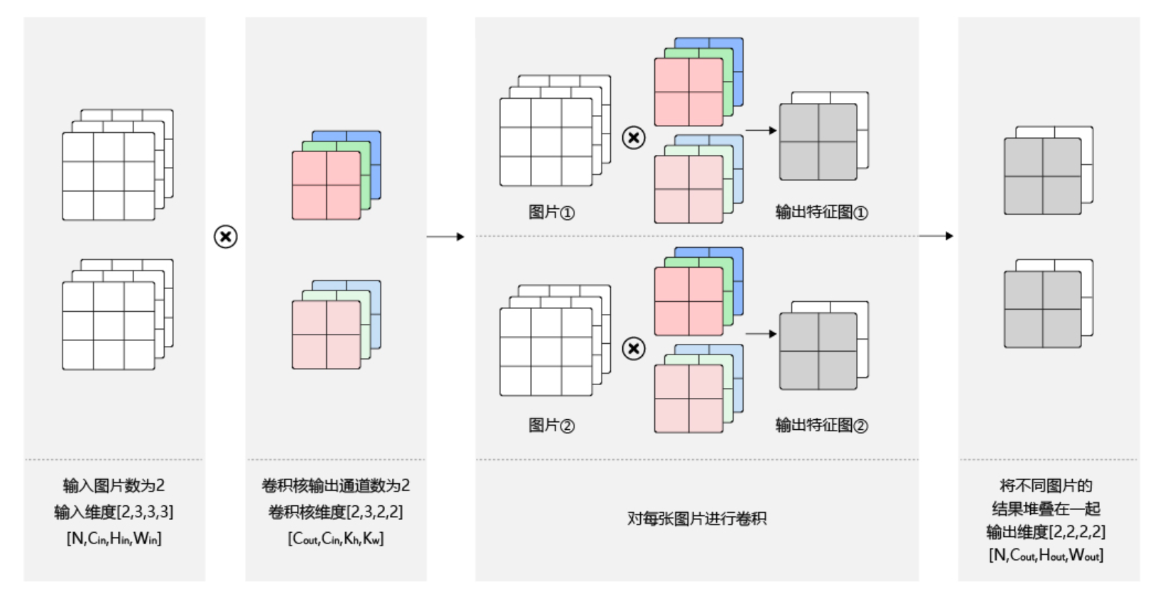
# 单层卷积网络
f^{[l]}$$ 第l层filter size $$p^{[l]}$$ 第l层padding size $$s^{[l]}$$ 第l层stride $$n_c^{[l]} $$filter数量 $$f^{[l]}*f^{[l]}*n_c^{[l-1]}$$ 每个filter大小 $$a^{[l]}->n_H^{[l]}*n_W^{[l]}*n_c^{[l]}
weight:$$f{[l]}*f^{[l]}*n_c[l-1]}*n_c$$
bias:$$(1,1,1,n_c^{[l]})$$
Input :$$n^[l-1]}_H \times n_W \times n_C^{[l-1]}$$
output: $$n^[l]}_H \times n_W \times n_C^{[l]}$$
n_H^{[l]}=\frac{n^{[l-1]}_H+2p^{[l]}-f^{[l]}}{s^{[l]}}$$,向下取整 $$n_W^{[l]}=\frac{n^{[l-1]}_W+2p^{[l]}-f^{[l]}}{s^{[l]}}$$,向下取整 #### 卷积网络 - convolution layer - pooling layer - fully connected layer #### 池化层 Max pooling 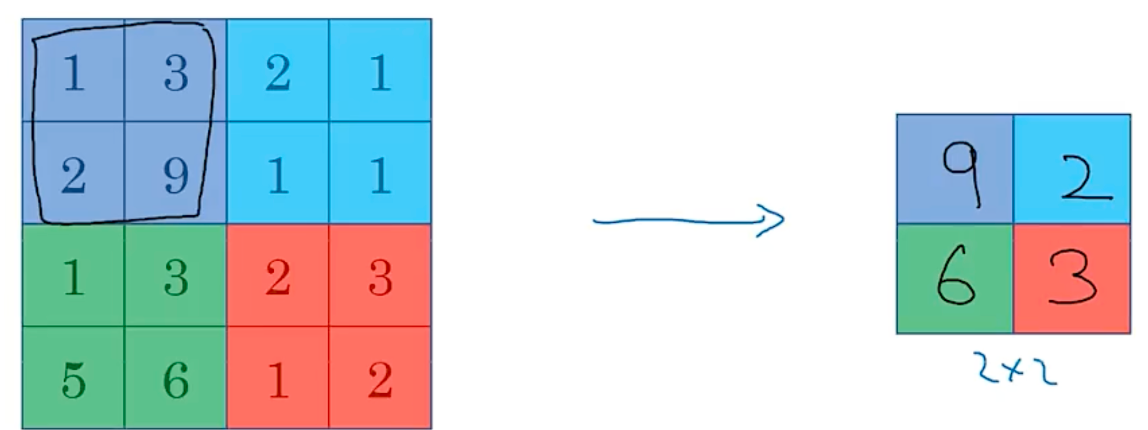 average pooling 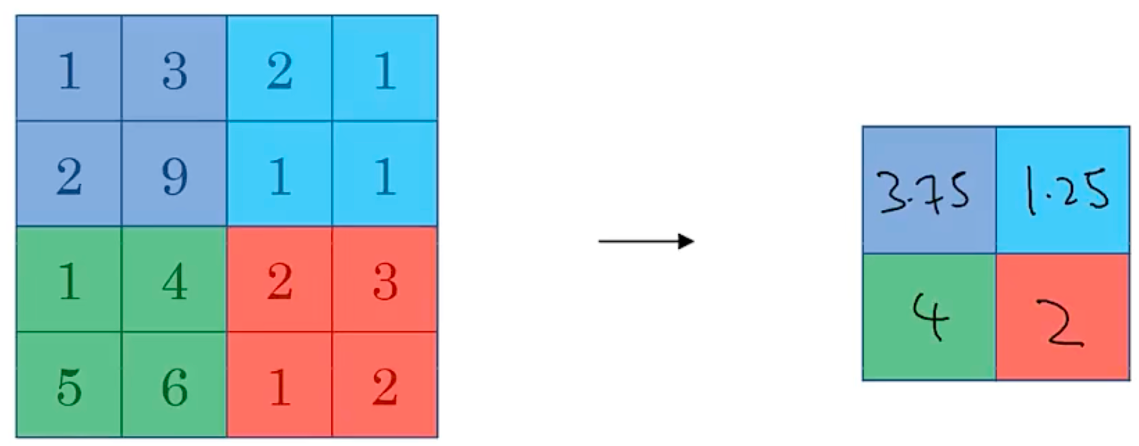 - 平均池化。这里使用大小为2×2的池化窗口,每次移动的步幅为2,对池化窗口覆盖区域内的像素取平均值,得到相应的输出特征图的像素值。 - 如图10(b):最大池化。对池化窗口覆盖区域内的像素取最大值,得到输出特征图的像素值。当池化窗口在图片上滑动时,会得到整张输出特征图。池化窗口的大小称为池化大小,用𝑘ℎ×𝑘𝑤表示。在卷积神经网络中用的比较多的是窗口大小为2×2,步幅为2的池化 在卷积神经网络中,通常使用2×2大小的池化窗口,步幅也使用2,填充为0,则输出特征图的尺寸为: 𝐻𝑜𝑢𝑡=𝐻/2 𝑊𝑜𝑢𝑡=𝑊/2 神经网络非常深的时候,可能会使用平均池化 一般情况大部分使用max pooling,最大池化一般不使用padding 池化没有参数可以学习,是固定参数 随着神经网络深入,nh和nw会减少,channel会增加 对于f=5,filter=6,参数=6*(5*5+1)=156,参数小 参数小的原因是可以参数共享,拥有稀疏连接 通过这种方式的池化,输出特征图的高和宽都减半,但通道数不会改变。由于池化层是使用某一位置的相邻输出的总体统计特征代替网络在该位置的输出,所以其好处是当输入数据做出少量平移时,经过池化运算后的大多数输出还能保持不变。比如:当识别一张图像是否是人脸时,我们需要知道人脸左边有一只眼睛,右边也有一只眼睛,而不需要知道眼睛的精确位置,这时候通过汇聚某一片区域的像素点来得到总体统计特征会显得很有用。这也就体现了池化层的平移不变特性。 随着神经网络的发展,出现更多池化方法,比如SSPNet提出了空间金字塔池化(Spatial Pyramid Pooling,SPP),对于不同尺寸的输入采用不同的滑窗大小和步长,从而确保输出尺寸相同,这样有利于提取不同尺寸的图像特征信息。全局平均池化(Global Average Pooling,GAP)第一次出现在论文Network in Network中,和Average Pooling的区别是对整个特征图求平均值,减少特征的丢失。除此之外还有Global Max Pooling、NetVLAD池化、随机池化、重叠池化、RoI池化等。 #### 经典网络 LeNet-5 AlexNet 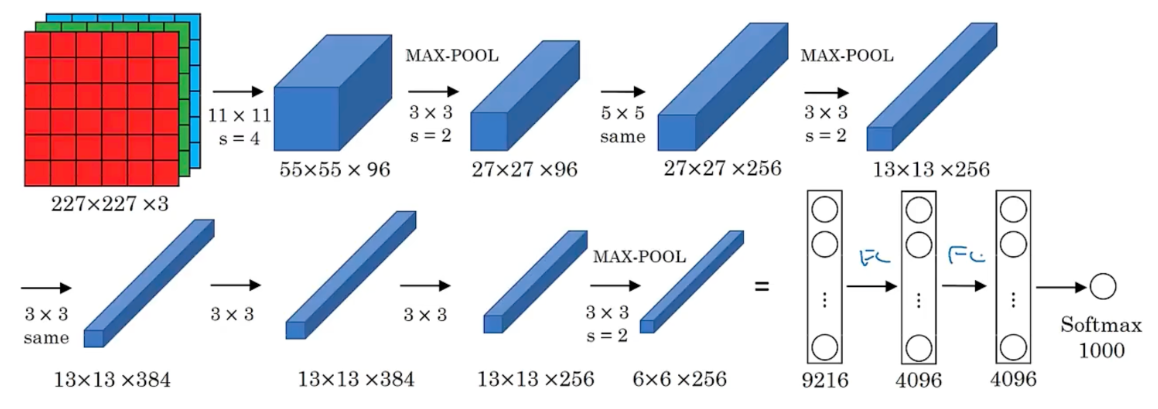 VGG ResNet Inception #### Resnet 残差连接(Residual Connection)是一种通过引入 “捷径”(Shortcut)或 “跳跃连接”(Skip Connection)来缓解深度神经网络训练难题的技术。 在深度学习中,理论上增加网络层数可以提升模型的表达能力,但实际训练中会面临以下问题: 梯度消失 / 爆炸:深层网络中,梯度反向传播时经过多层非线性激活函数,可能导致梯度逐渐衰减或激增,使得网络难以优化。 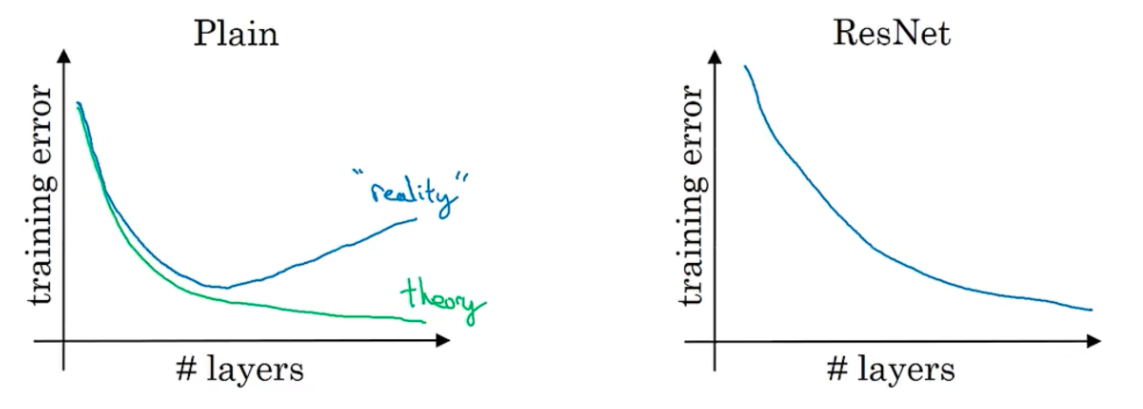 在神经网络中,残差连接(Residual Connection)就像这样一条“捷径”:**它让信息在经历中间复杂的处理步骤的同时,还直接从输入传递到输出,以合并信息。** 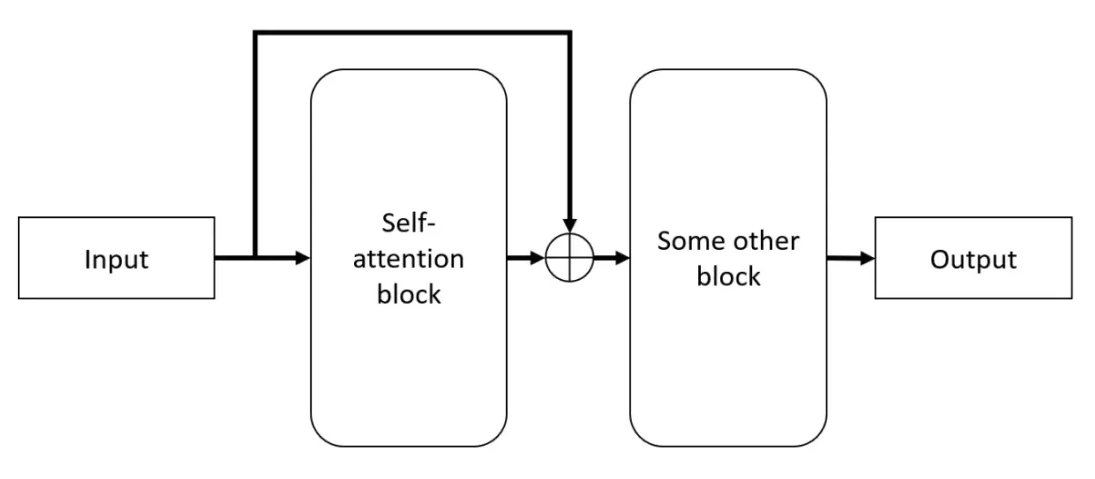 输出 = F(x) + x 这个方式在transformer中得到了深入应用  这样,每一层都把“原始信息”直接传递下去,就能够确保“大方向”不偏。而且即使 F(x) 表现不佳,网络依然可以退化为“恒等映射”,起码不会破坏输入信息。这也让梯度反向传播更稳定,因为梯度可以沿着残差路径“直达”前层,减少衰减。 可以与输入相加的原因是,它们“形状一致”,也就是“大小相同”。 #### 残差单元 由于ResNet每层都存在直连的旁路,相当于每一层都和最终的损失有“直接对话”的机会,自然可以更好的解决梯度弥散的问题。残差块的具体设计方案,这种设计方案也常称作瓶颈结构(BottleNeck)。1*1的卷积核可以非常方便的调整中间层的通道数,在进入3*3的卷积层之前减少通道数(256->64),经过该卷积层后再恢复通道数(64->256),可以显著减少网络的参数量。这个结构(256->64->256)像一个中间细,两头粗的瓶颈,所以被称为“BottleNeck”。 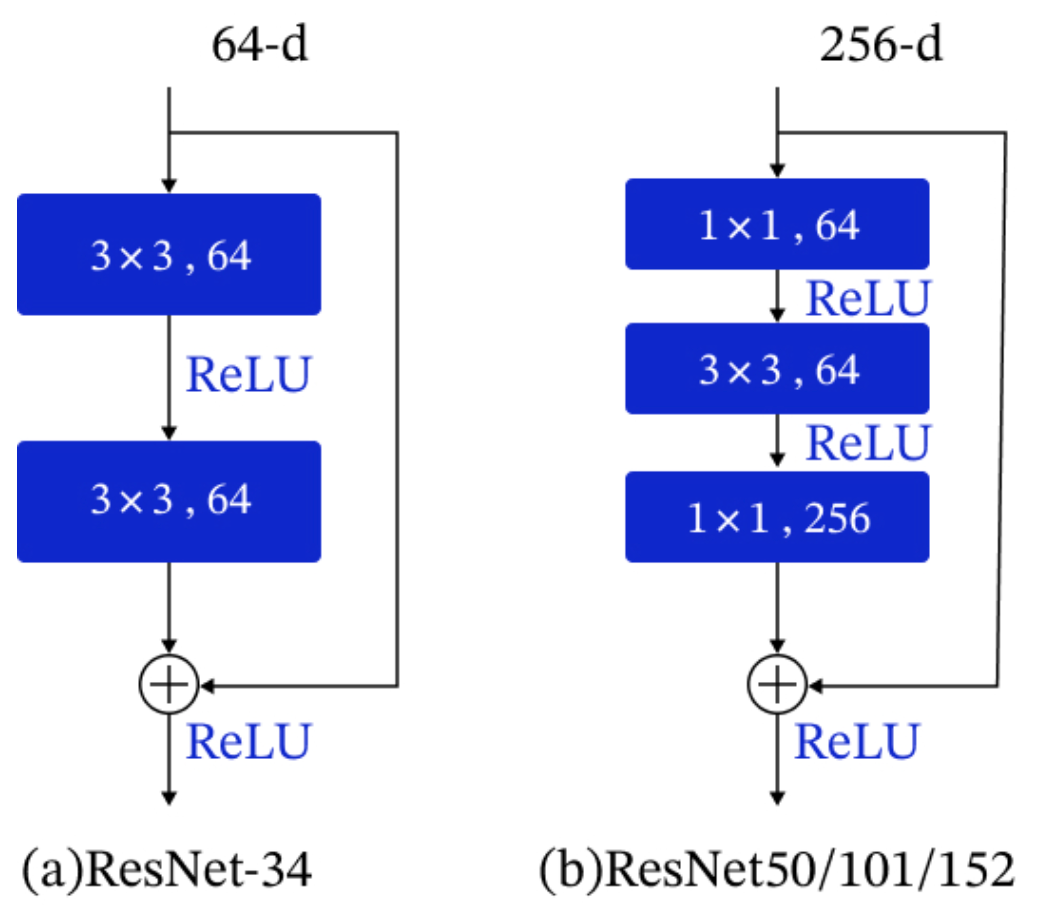 1 × 1卷积:与标准卷积完全一样,唯一的特殊点在于卷积核的尺寸是1 × 1,也就是不去考虑输入数据局部信息之间的关系,而把关注点放在不同通道间。通过使用1 × 1卷积,可以起到如下作用: - 实现信息的跨通道交互与整合。考虑到卷积运算的输入输出都是3个维度(宽、高、多通道),所以1 × 1卷积实际上就是对每个像素点,在不同的通道上进行线性组合,从而整合不同通道的信息; - 对卷积核通道数进行降维和升维,减少参数量。经过1 × 1卷积后的输出保留了输入数据的原有平面结构,通过调控通道数,从而完成升维或降维的作用; - 利用1 × 1卷积后的非线性激活函数,在保持特征图尺寸不变的前提下,大幅增加非线性。 #### inception #### batch-norm 其目的是对神经网络中间层的输出进行标准化处理,使得中间层的输出更加稳定。 通常我们会对神经网络的数据进行标准化处理,**处理后的样本数据集满足均值为0,方差为1的统计分布**,这是因为当输入数据的分布比较固定时,有利于算法的稳定和收敛。对于深度神经网络来说,由于参数是不断更新的,即使输入数据已经做过标准化处理,但是对于比较靠后的那些层,其接收到的输入仍然是剧烈变化的,通常会导致数值不稳定,模型很难收敛。BatchNorm能够使神经网络中间层的输出变得更加稳定,并有如下三个优点: - 使学习快速进行(能够使用较大的学习率) - 降低模型对初始值的敏感性 - 从一定程度上抑制过拟合 BatchNorm主要思路是在训练时以mini-batch为单位,对神经元的数值进行归一化,使数据的分布满足均值为0,方差为1。具体计算过程如下: **1. 计算mini-batch内样本的均值** $$\mu_B \leftarrow \frac{1}{m}\sum_{i=1}^mx^{(i)}其中 $$x^{(i)}$$ 表示 mini-batch 中的第 $$i$$ 个样本。
例如输入 mini-batch 包含 3 个样本,每个样本有 2 个特征,分别是:
对每个特征分别计算 mini-batch 内样本的均值:
则样本均值是:
2. 计算 mini-batch 内样本的方差
上面的计算公式先计算一个批次内样本的均值 $$\mu_B$$ 和方差 $$\sigma_B^2$$,然后再对输入数据做归一化,将其调整成均值为 0,方差为 1 的分布。
对于上述给定的输入数据 $$x^(1)}, x, x^{(3)}$$,可以计算出每个特征对应的方差:
则样本方差是:
3. 计算标准化之后的输出
其中 $$\epsilon$$ 是一个微小值(例如 $$1e-7$$),其主要作用是为了防止分母为 0。
对于上述给定的输入数据 $$x^(1)}, x, x^{(3)}$$,可以计算出标准化之后的输出:
如果强行限制输出层的分布是标准化的,可能会导致某些特征模式的丢失,所以在标准化之后,BatchNorm 会紧接着对数据做缩放和平移。
其中 $$\gamma$$ 和 $$\beta$$ 是可学习的参数,可以赋初始值 $$\gamma = 1, \beta = 0$$,在训练过程中不断学习调整。
- 当输入数据形状是 [𝑁,𝐶,𝐻,𝑊] 时, 一般对应卷积层的输出,示例代码如下所示。
这种情况下会沿着 C 这一维度进行展开,分别对每一个通道计算 N 个样本中总共𝑁×𝐻×𝑊个像素点的均值和方差,数据和参数对应如下:
- 输入 x, [N, C, H, W]
- 输出 y, [N, C, H, W]
- 均值 𝜇𝐵,[C,]
- 方差 𝜎2𝐵, [C,]
- 缩放参数𝛾, [C,]
- 平移参数𝛽, [C,]
BatchNorm 的变体包括:层归一化 (Layer Normalization, LN)、组归一化 (Group Normalization, GN)、实例归一化 (Instance Normalization, IN),通过下图进行比较,
其中 N 是 batch size、H 和 W 分别表示特征图的高度和宽度、C 表示特征图的通道数,蓝色像素表示使用相同的均值和方差进行归一化:
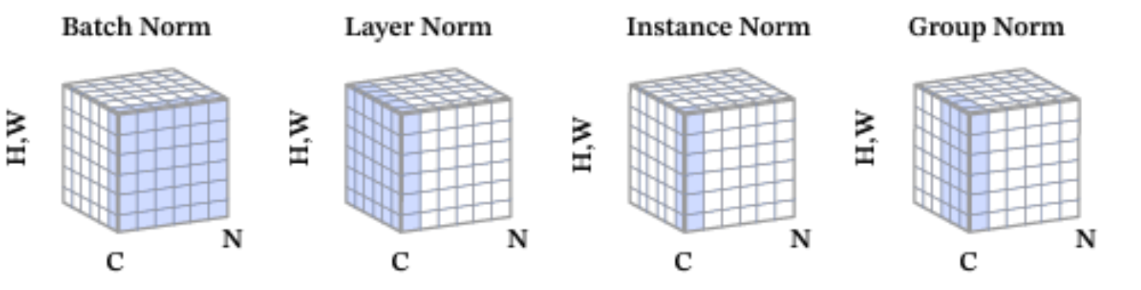
Layer Normalization(层归一化)和 Batch Normalization(批归一化)是深度学习中常用的两种归一化技术,它们的核心目标都是加速模型训练并提高稳定性,但应用方式和场景有显著区别。以下是详细对比:
# 核心区别
| 对比项 | Batch Normalization (BN) | Layer Normalization (LN) |
|---|---|---|
| 归一化维度 | 对批量(Batch)中所有样本的同一特征维度进行归一化 | 对单个样本的所有特征维度进行归一化 |
| 参数依赖 | 依赖批量大小(Batch Size),批量较小时效果差 | 不依赖批量大小,适合批量小或序列长度可变的场景 |
| 应用场景 | 计算机视觉(CV)任务(如 CNN) | 自然语言处理(NLP)任务(如 Transformer、RNN) |
| 计算方式 | 对每个特征维度计算均值和方差: $$\mu_c = \frac1}{m} \sum_{i=1}$$ | 对每个样本计算均值和方差: $$\mu_i = \frac1}{d} \sum_{c=1}$$ |
# 数学原理对比
# Batch Normalization
对于输入 $$x \in \mathbbR}$$ m 为批量大小,d 为特征维度),对每个特征维度 c 计算均值和方差:
归一化后的值:
其中 $$\epsilon$$ 是防止分母为零的小常数。
最终输出:$$y_{i,c} = \gamma_c \hat {x}_{i,c} + \beta_c $$,其中 $$\gamma$$ 和 $$ \beta$$ 是可学习的缩放和平移参数。
# Layer Normalization
对于输入 $$ x \in \mathbbR} $$,对每个样本 i 的所有特征维度计算均值和方差:
归一化后的值:
同样通过 $$\gamma$$ 和 $$\beta$$ 进行缩放和平移(每个样本共享一组参数)。
# 可视化对比
假设输入是一个批量的词向量(形状为 $$ \text {Batch Size} \times \text {Sequence Length} \times \text {Hidden Size} $$
- Batch Normalization:对所有样本的同一位置的特征(如所有样本的第 3 个词向量的第 5 个维度)计算均值和方差。
- Layer Normalization:对每个样本的所有特征(如单个样本的所有词向量的所有维度)计算均值和方差。
# 优缺点与适用场景
| 方法 | 优点 | 缺点 | 典型应用 |
|---|---|---|---|
| Batch Norm | - 加速训练,缓解梯度消失 - 提高模型泛化能力 |
- 依赖批量大小,小批量时不稳定 - 不适合序列长度可变的任务 |
CNN(如 ResNet、VGG) |
| Layer Norm | - 不依赖批量,适合小批量或在线学习 - 对序列长度变化鲁棒 |
- 对某些计算机视觉任务效果可能不如 BN | Transformer、RNN(如 LSTM、GRU) |
# 总结:如何选择?
- 优先使用 Batch Norm:当批量大小较大且数据分布相对稳定时(如 CV 任务),BN 能有效加速训练。
- 优先使用 Layer Norm:
- 当批量较小时(如医疗图像、小样本学习);
- 当处理序列数据(如 NLP 中的文本)时,序列长度可变,LN 更稳定;
- 当模型需要在线学习或处理单个样本时。
此外,还有 Group Normalization(GN)、Instance Normalization(IN)等变体,它们的核心区别在于归一化维度的选择不同。
# 数据增强
垂直轴镜像 - mirroring
random cropping
Rotation
Shearing
Local warping
color shifting
# 目标定位
b_x,b_y,b_h,b_w$$,class label 以图片左上角作为0,0,bx,by为定位中心点,bh,bw为物体宽高.pc是否是物体,c1-c3为物体分类 1 - pedestrian 2 - car 3 - motorcycle 4 - background $$y=\begin{bmatrix} p_c\\b_x\\b_y\\b_h\\b_w\\c_1\\c_2\\c_3 \end{bmatrix}
# 卷积滑动窗口

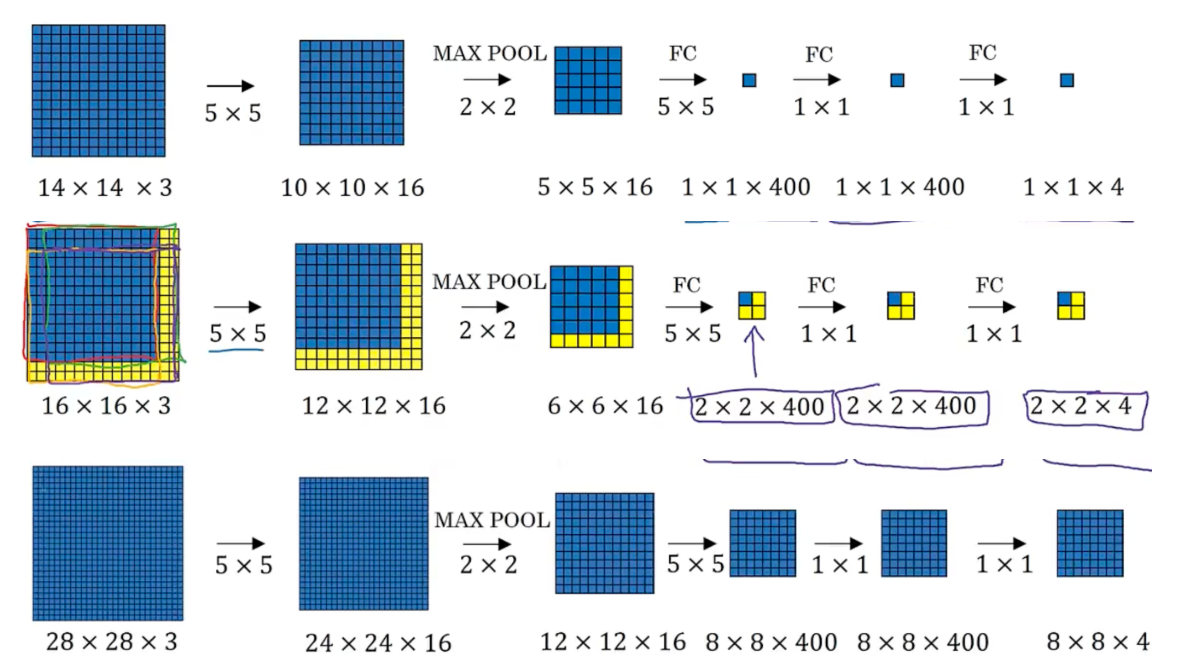
# YOLO
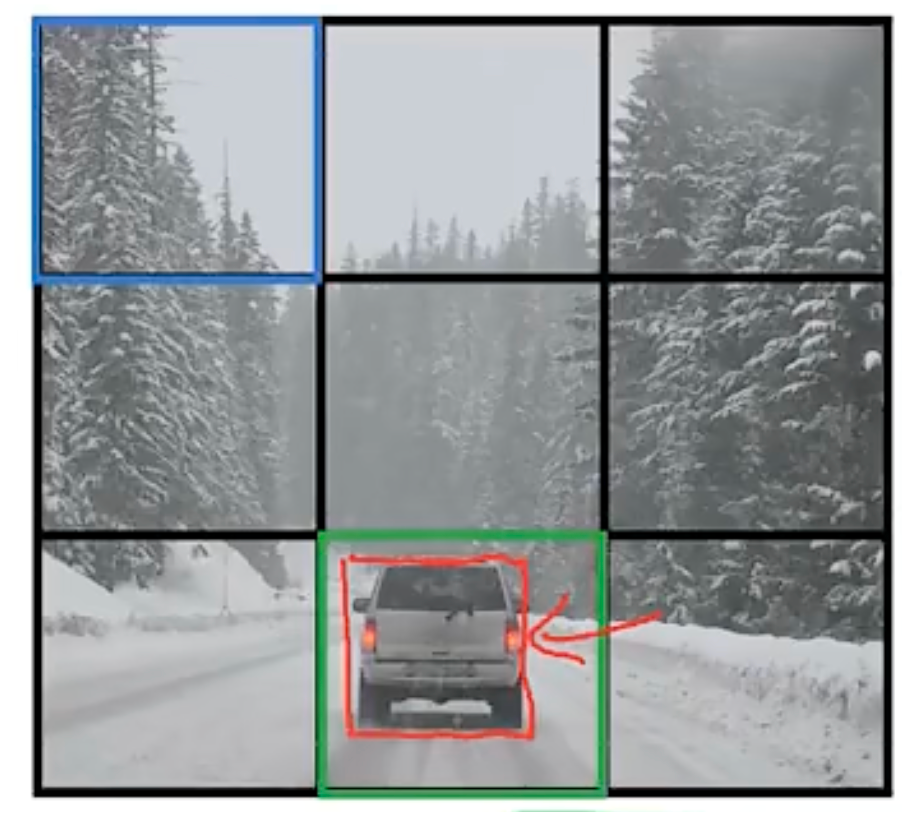
将图像分成若干个 grid,对于每个 grid 应用 label
分配物体中点给对应 grid
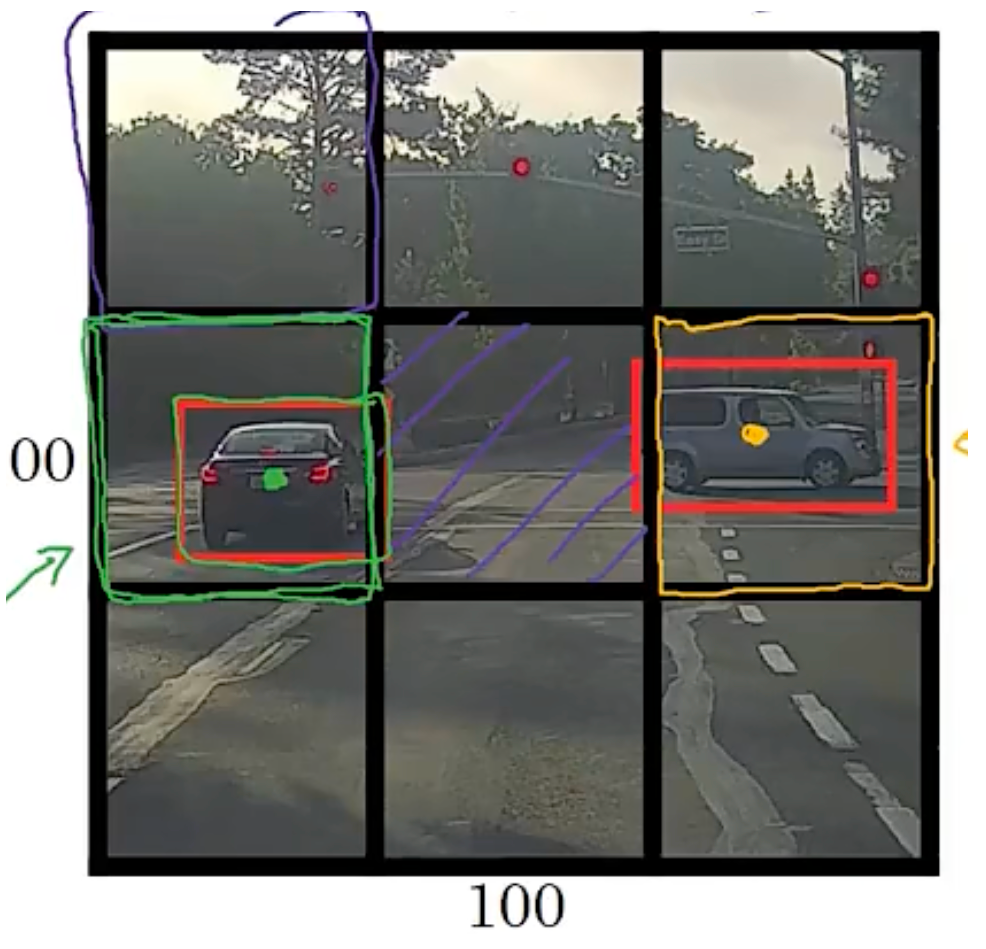
IOU

y 是 332*8 ,2 是 anchor,8=5+3,即三种可能得类型
对每个 3*3 格子计算 y
运行非极大值预测
For each grid call, get 2 predicted bounding boxes.
Get rid of low probability predictions.
For each class (pedestrian, car, motorcycle) use non-max suppression to generate final predictions.
# R-CNN
region-cnn
只选择几个窗口运行 cnn
# one-shot
degree of difference ,if d(img1,img2) <= t same
else
# siamese
Parameters of NN define an encoding f(x(t))
Learn parameters so that:
- If xi,xj are the same person, ||fxi-fxj||^2 is small
- If xi,xj are different person, ||f(xi))-f(xj))||2is large.
# triple loss
# NLP
NN:https://playground.tensorflow.org/#activation=tanh&batchSize=10&dataset=circle®Dataset=reg-plane&learningRate=0.03®ularizationRate=0&noise=0&networkShape=4,2&seed=0.29103&showTestData=false&discretize=false&percTrainData=50&x=true&y=true&xTimesY=false&xSquared=false&ySquared=false&cosX=false&sinX=false&cosY=false&sinY=false&collectStats=false&problem=classification&initZero=false&hideText=false
卷积操作图示:https://setosa.io/ev/image-kernels/
GPU 对比页面用 AI 工具生成的代码:https://www.blackbox.ai/
手写数字识别过程演示:https://felixzhang00.github.io/DL/mnist/
3D CNN 网络可视化:https://adamharley.com/nn_vis/cnn/3d.html
word embedding:https://ronxin.github.io/wevi/
embedding:https://projector.tensorflow.org/
# RNN
# sequence data
speech recognition
music generation
sentiment classifcation
DNA sequence analysis
machine translation
# notation
x^{}$$ t索引位置 $$T_x$$ = 9 $$y^{}x^{(i)}$$ 第i个训练集中第t个元素 $$T_x^{(i)} 第i个train—set中输入序列长度
presenting words
创建一个词表,假设有 1w 词。用 one-hot 表示每一个词
one-hot 表示 abandon
one-hot 维度与词表维度一致
# RNN
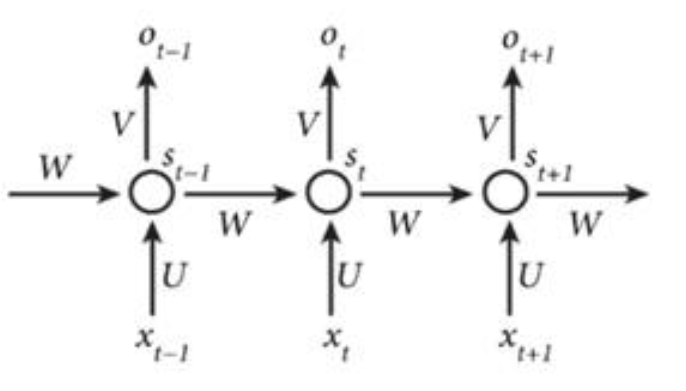
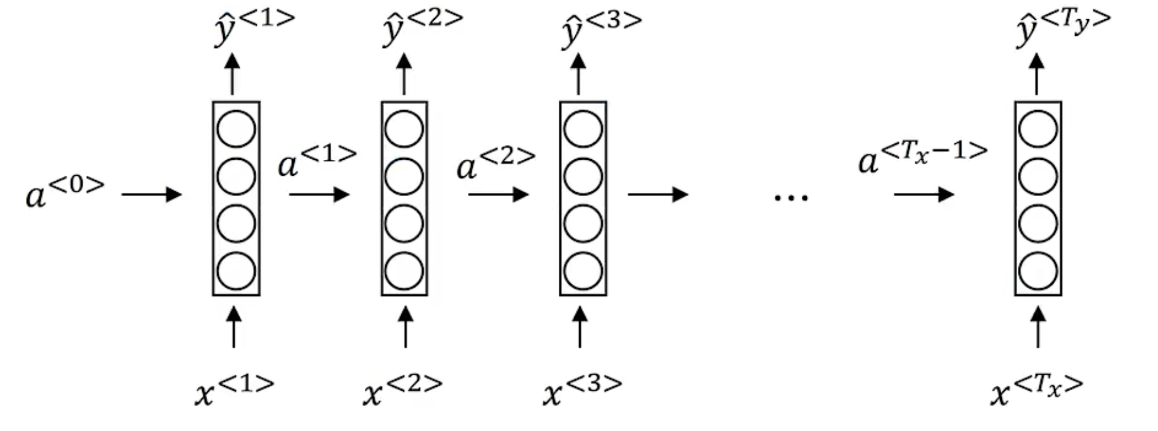
假设给定任意一句话 [x0,x1,…,xn],其中每个 xi 都代表了一个词,如 “我,爱,人工,智能”。循环神经网络从左到右逐词阅读这个句子,并不断调用一个相同的 RNN Cell 来处理时序信息。每阅读一个单词,循环神经网络会先将本次输入的单词通过 embedding lookup 转换为一个向量表示。再把这个单词的向量表示和这个模型内部记忆的向量 h 融合起来,形成一个更新的记忆。最后将这个融合后的表示输出出来,作为它当前阅读到的所有内容的语义表示。当循环神经网络阅读过整个句子之后,我们就可以认为它的最后一个输出状态表示了整个句子的语义信息。
# rnn 前向传播
a^{<1>}=g_1(W_{aa}a^{<0>}+W_{ax}x^{<1>}+b_a)$$ g 一般是tanh或relu $$\hat{y}^{<1>}=g_2(W_{ya}a^{<1>}+b_y)$$ g可以是sigmoid或softmax tanh函数是一个值域为(-1,1)的函数,其作用是长期维持内部记忆在一个固定的数值范围内,防止因多次迭代更新导致数值爆炸。同时tanh的导数是一个平滑的函数,会让神经网络的训练变得更加简单。 另一种表示方法 $$a^{
# rnn 反向传播
# 不同 rnn
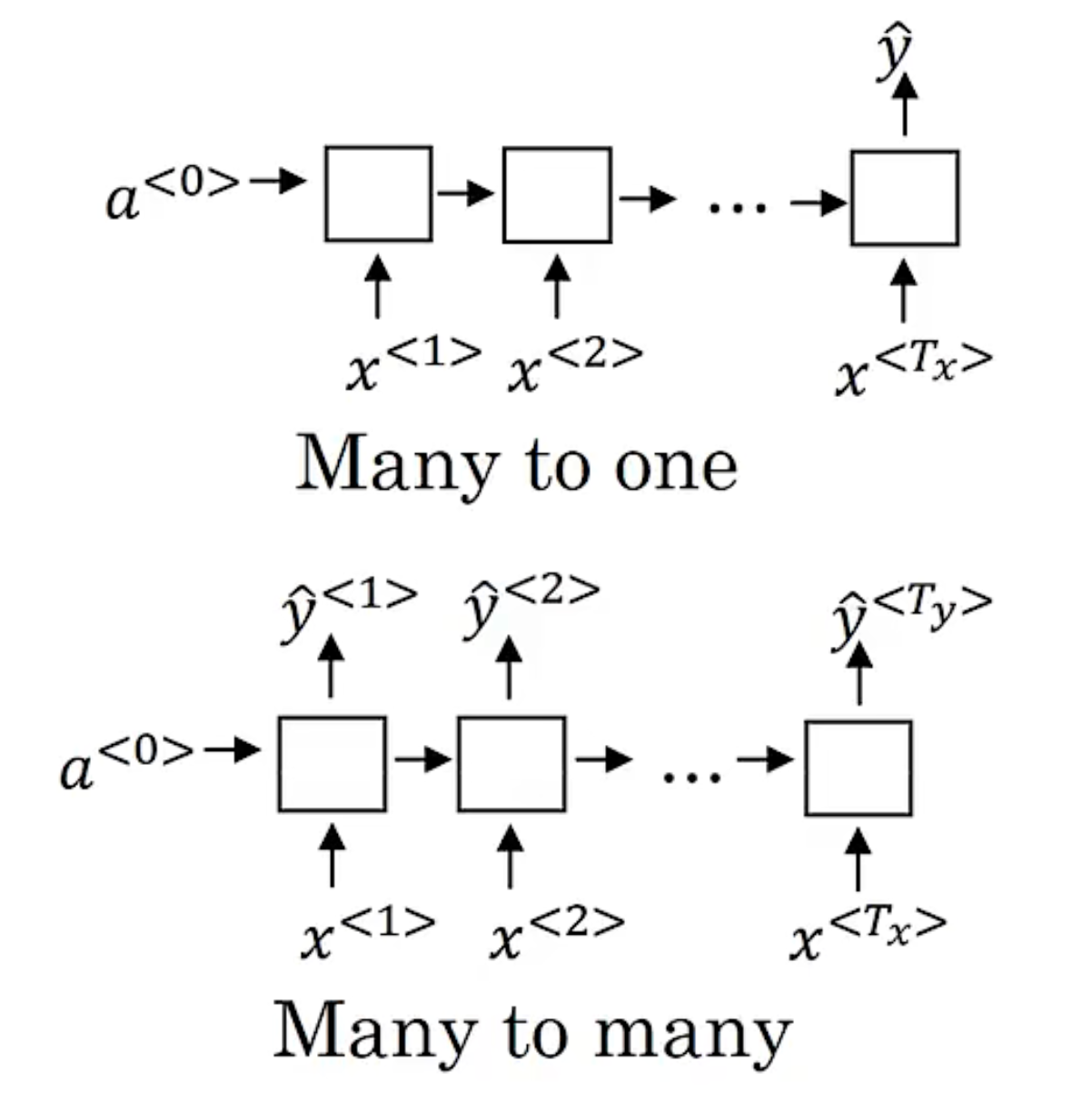
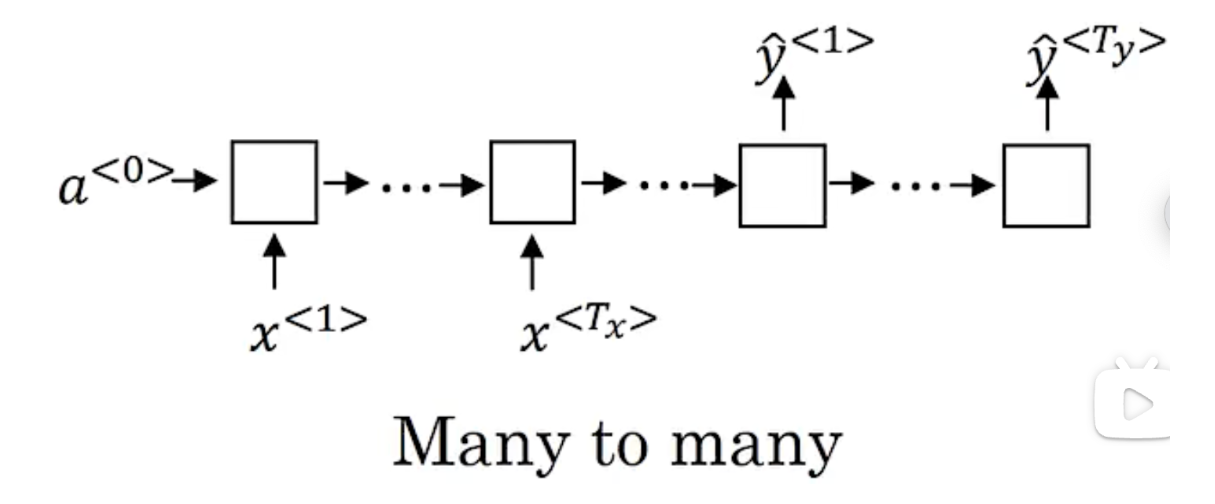
many-to-many architecture
many-to-one architecture
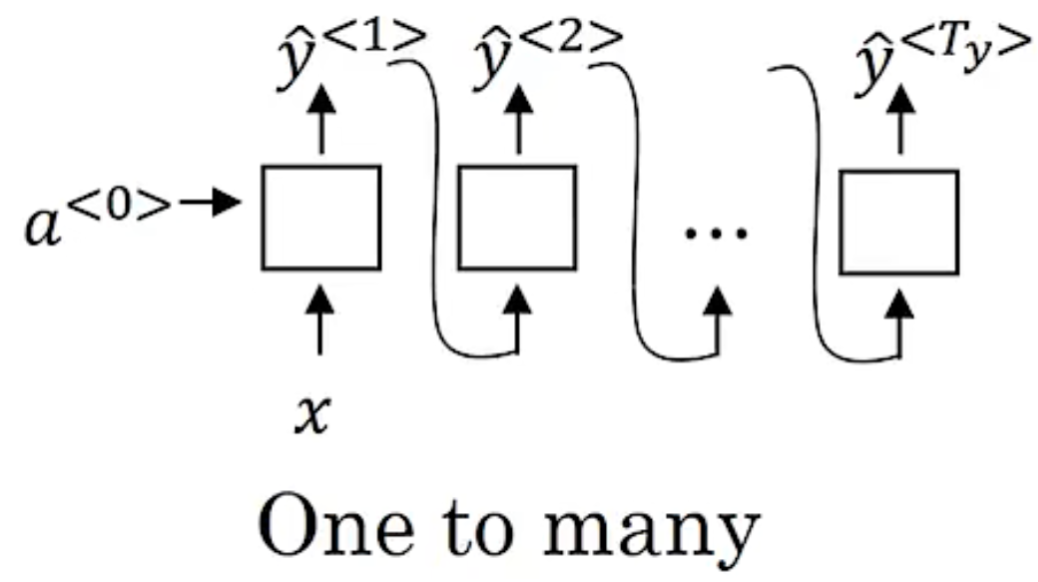
one-to-one
# 语言模型
输入一个序列,$$y^}$$, 估计概率 $$P (y)$$
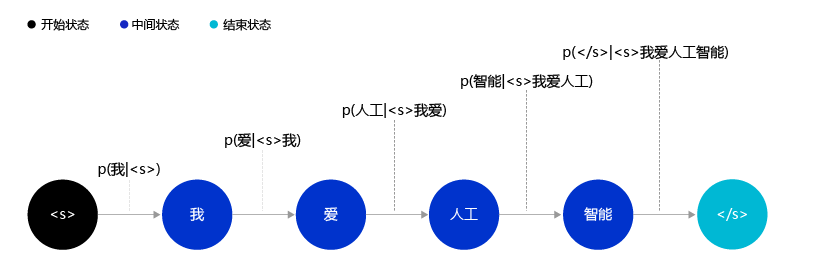
循环神经网络开始从左到右阅读这个句子,在未经过任何阅读之前,循环神经网络中的记忆向量是空白的。其处理逻辑如下:
- 网络阅读单词 “我”,并把单词 “我” 的向量表示和空白记忆相融合,输出一个向量 h1,用于表示 “空白 + 我” 的语义。
- 网络开始阅读单词 “爱”,这时循环神经网络内部存在 “空白 + 我” 的记忆。循环神经网络会将 “空白 + 我” 和 “爱” 的向量表示相融合,并输出 “空白 + 我 + 爱” 的向量表示 h2,用于表示 “我爱” 这个短语的语义信息。
- 网络开始阅读单词 “人工”,同样经过融合之后,输出 “空白 + 我 + 爱 + 人工” 的向量表示 h3h3,用于表示 “空白 + 我 + 爱 + 人工” 语义信息。
- 最终在网络阅读了 “智能” 单词后,便可以输出 “我爱人工智能” 这一句子的整体语义信息。
# GRU
GRU 是一种神经网络,旨在处理顺序数据,例如时间序列数据或自然语言文本。然而,与传统的 RNN 不同,GRU 包含一种门控机制,允许网络根据输入数据有选择地更新其隐藏状态。
具体来说,一个 GRU 包括两个门:重置门和更新门。重置门确定要忘记多少先前的隐藏状态,而更新门确定将多少新输入合并到更新的隐藏状态中。通过允许网络根据输入数据有选择地保留或忘记信息,GRU 可以学习比传统 RNN 架构更有效地建模长期依赖性。
The cat , which … ,was full.
# LSTM
当阅读很长的序列时,网络内部的信息会变得越来越复杂,甚至会超过网络的记忆能力,使得最终的输出信息变得混乱无用。长短时记忆网络(Long Short-Term Memory,LSTM)内部的复杂结构正是为处理这类问题而设计的
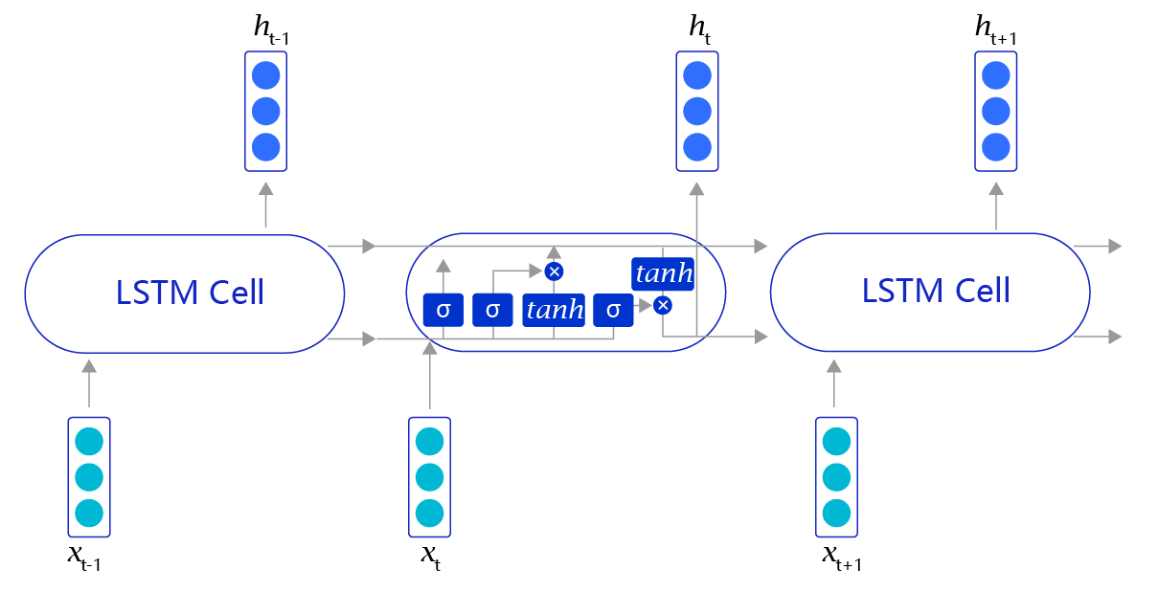
长短时记忆网络的 Cell 有三个输入:
- 这个网络新看到的输入信号,如下一个单词,记为 xt, 其中 xt 是一个向量,t 代表了当前时刻。
- 这个网络在上一步的输出信号,记为 ht−1,这是一个向量,维度同 xt 相同。
- 这个网络在上一步的记忆信号,记为 ct−1,这是一个向量,维度同 xt 相同。
在每个处理单元内部,加入了输入门、输出门和遗忘门的设计,三者有明确的任务分工:
- 输入门:控制有多少输入信号会被融合;$$i_t$$
- 遗忘门:控制有多少过去的记忆会被遗忘;$$f_t$$
- 输出门:控制多少处理后的信息会被输出;$$o_t$$
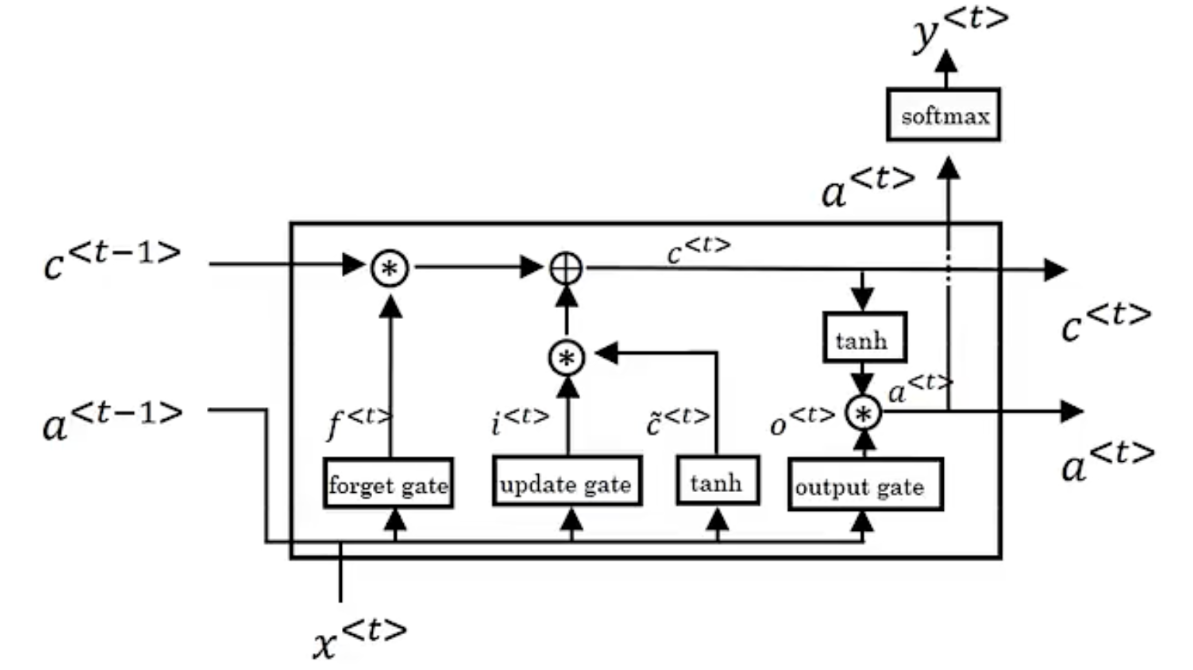
通过学习这些门的权重设置,长短时记忆网络可以根据当前的输入信号和记忆信息,有选择性地忽略或者强化当前的记忆或是输入信号,帮助网络更好地学习长句子的语义信息:
- 记忆信号:$$ c_t = f_t \cdot c_{t - 1} + i_t \cdot g_t $$
- 输出信号:$$ h_t = o_t \cdot \tanh (c_t)$$
# 双向 rnn
# word embedding
在自然语言处理任务中,词向量(Word Embedding)是表示自然语言里单词的一种方法,即把每个词都表示为一个 N 维空间内的点,即一个高维空间内的向量。通过这种方法,实现把自然语言计算转换为向量计算。
先把每个词(如 queen,king 等)转换成一个高维空间的向量,这些向量在一定意义上可以代表这个词的语义信息。再通过计算这些向量之间的距离,就可以计算出词语之间的关联关系,从而达到让计算机像计算数值一样去计算自然语言的目的。
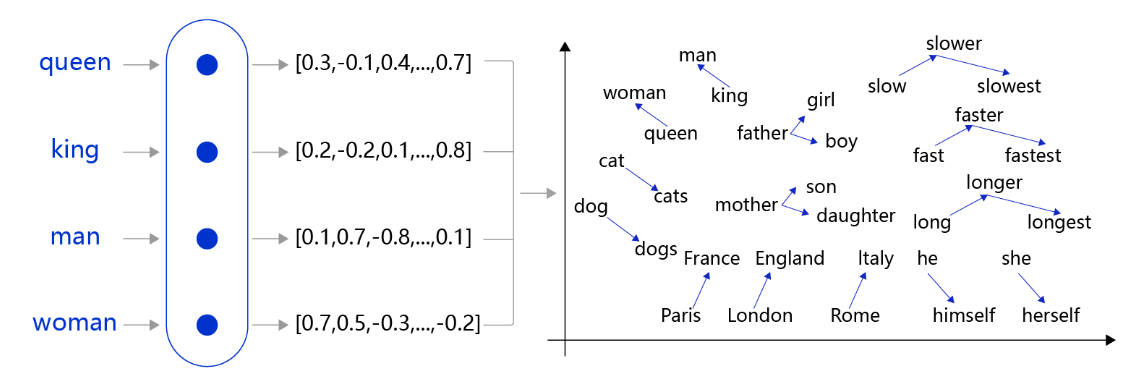
我们可以维护一个查询表。表中每一行都存储了一个特定词语的向量值,每一列的第一个元素都代表着这个词本身,以便于我们进行词和向量的映射(如 “我” 对应的向量值为 [0.3,0.5,0.7,0.9,-0.2,0.03] )。给定任何一个或者一组单词,我们都可以通过查询这个 excel,实现把单词转换为向量的目的,这个查询和替换过程称之为 Embedding Lookup。
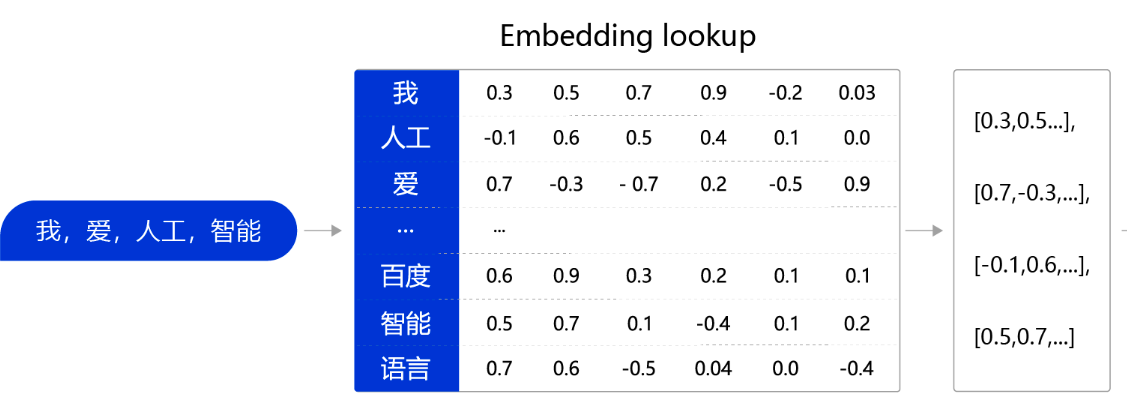
上述过程也可以使用一个字典数据结构实现。事实上如果不考虑计算效率,使用字典实现上述功能是个不错的选择。然而在进行神经网络计算的过程中,需要大量的算力,常常要借助特定硬件(如 GPU)满足训练速度的需求。GPU 上所支持的计算都是以张量(Tensor)为单位展开的,因此在实际场景中,我们需要把 Embedding Lookup 的过程转换为张量计算
O_{1234}$$ one-hot key $$E \cdot O_j=e_j=embedding~for~word~j
把 Embedding Lookup 的过程转换为张量计算的流程如下:
- 通过查询字典,先把句子中的单词转换成一个 ID(通常是一个大于等于 0 的整数),这个单词到 ID 的映射关系可以根据需求自定义(如图 3 中,我 =>1, 人工 =>2,爱 =>3,…)。
- 得到 ID 后,再把每个 ID 转换成一个固定长度的向量。假设字典的词表中有 5000 个词,那么,对于单词 “我”,就可以用一个 5000 维的向量来表示。由于 “我” 的 ID 是 1,因此这个向量的第一个元素是 1,其他元素都是 0([1,0,0,…,0]);同样对于单词 “人工”,第二个元素是 1,其他元素都是 0。用这种方式就实现了用一个向量表示一个单词。由于每个单词的向量表示都只有一个元素为 1,而其他元素为 0,因此我们称上述过程为 One-Hot Encoding。
- 经过 One-Hot Encoding 后,句子 “我,爱,人工,智能” 就被转换成为了一个形状为 4×5000 的张量,记为 VV。在这个张量里共有 4 行、5000 列,从上到下,每一行分别代表了 “我”、“爱”、“人工”、“智能” 四个单词的 One-Hot Encoding。最后,我们把这个张量 VV 和另外一个稠密张量 WW 相乘,其中 WW 张量的形状为 5000 × 128(5000 表示词表大小,128 表示每个词的向量大小)。经过张量乘法,我们就得到了一个 4×128 的张量,从而完成了把单词表示成向量的目的。
# word2vec
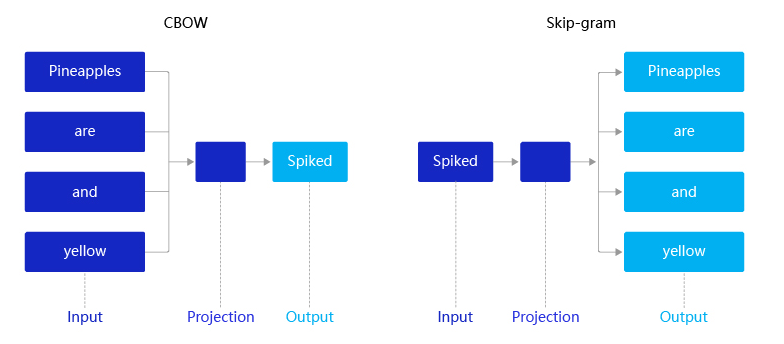
2013 年,Mikolov 提出的经典 word2vec 算法就是通过上下文来学习语义信息。word2vec 包含两个经典模型:CBOW(Continuous Bag-of-Words)和 Skip-gram。
- CBOW:通过上下文的词向量推理中心词。
- Skip-gram:根据中心词推理上下文。
假设有一个句子 “Pineapples are spiked and yellow”,两个模型的推理方式如下:
- 在 CBOW 中,先在句子中选定一个中心词,并把其它词作为这个中心词的上下文。 CBOW 所示,把 “Spiked” 作为中心词,把 “Pineapples、are、and、yellow” 作为中心词的上下文。在学习过程中,使用上下文的词向量推理中心词,这样中心词的语义就被传递到上下文的词向量中,如 “Spiked → pineapple”,从而达到学习语义信息的目的。
- 在 Skip-gram 中,同样先选定一个中心词,并把其他词作为这个中心词的上下文。Skip-gram 所示,把 “Spiked” 作为中心词,把 “Pineapples、are、and、yellow” 作为中心词的上下文。不同的是,在学习过程中,使用中心词的词向量去推理上下文,这样上下文定义的语义被传入中心词的表示中,如 “pineapple → Spiked”, 从而达到学习语义信息的目的。
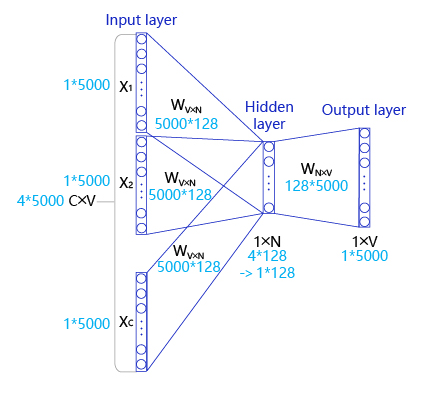
# CBOW
- 输入层: 一个形状为 C×V 的 one-hot 张量,其中 C 代表上线文中词的个数,通常是一个偶数,我们假设为 4;V 表示词表大小,我们假设为 5000,该张量的每一行都是一个上下文词的 one-hot 向量表示,比如 “Pineapples, are, and, yellow”。
- 隐藏层: 一个形状为 V×N 的参数张量 W1,一般称为 word-embedding,N 表示每个词的词向量长度,我们假设为 128。输入张量和 word embedding W1 进行矩阵乘法,就会得到一个形状为 C×N 的张量。综合考虑上下文中所有词的信息去推理中心词,因此将上下文中 C 个词相加得一个 1×N 的向量,是整个上下文的一个隐含表示。
- 输出层: 创建另一个形状为 N×V 的参数张量,将隐藏层得到的 1×N 的向量乘以该 N×V 的参数张量,得到了一个形状为 1×V 的向量。最终,1×V 的向量代表了使用上下文去推理中心词,每个候选词的打分,再经过 softmax 函数的归一化,即得到了对中心词的推理概率:
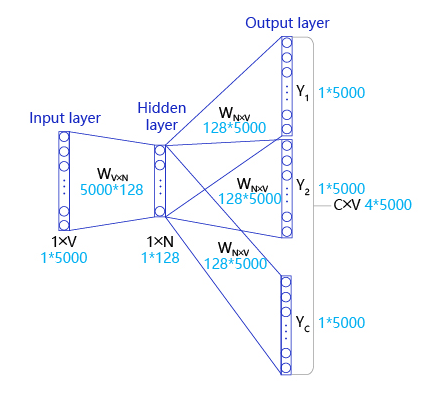
# skip-gram
- Input Layer(输入层):接收一个 one-hot 张量 V∈R1×vocab_size 作为网络的输入,里面存储着当前句子中心词的 one-hot 表示。
- Hidden Layer(隐藏层):将张量 V 乘以一个 word embedding 张量 W1∈Rvocab_size×embed_size,并把结果作为隐藏层的输出,得到一个形状为 R1×embed_size 的张量,里面存储着当前句子中心词的词向量。
- Output Layer(输出层):将隐藏层的结果乘以另一个 word embedding 张量 W2∈Rembed_size×vocab_size,得到一个形状为 R1×vocab_size 的张量。这个张量经过 softmax 变换后,就得到了使用当前中心词对上下文的预测结果。根据这个 softmax 的结果,我们就可以去训练词向量模型。
在实际操作中,使用一个滑动窗口(一般情况下,长度是奇数),从左到右开始扫描当前句子。每个扫描出来的片段被当成一个小句子,每个小句子中间的词被认为是中心词,其余的词被认为是这个中心词的上下文。
softmax: $$p(t|c)=\frace}\sum_{j=1}e^e_c\theta}$$,$$\theta_{t} $$ 输出 t 的关联参数
\sum_{j=1}^{10000}$$使计算变得慢,使用二元softmax分类器。不需要对整个词汇表做求和 #### 负采样 然而在实际情况中,vocab_size通常很大(几十万甚至几百万),导致W0和W1也会非常大。对于W0而言,所参与的矩阵运算并不是通过一个矩阵乘法实现,而是通过指定ID,对参数W0进行访存的方式获取。然而对W1而言,仍要处理一个非常大的矩阵运算(计算过程非常缓慢,需要消耗大量的内存/显存)。为了缓解这个问题,通常采取负采样(negative_sampling)的方式来近似模拟多分类任务。此时新定义的W0和W1均为形状为[vocab_size, embedding_size]的张量。 假设有一个中心词c和一个上下文词正样本tp。在Skip-gram的理想实现里,需要最大化使用c推理tp的概率。在使用softmax学习时,需要最大化tp的推理概率,同时最小化其他词表中词的推理概率。之所以计算缓慢,是因为需要对词表中的所有词都计算一遍。然而我们还可以使用另一种方法,就是随机从词表中选择几个代表词,通过最小化这几个代表词的概率,去近似最小化整体的预测概率。比如,先指定一个中心词(如“人工”)和一个目标词正样本(如“智能”),再随机在词表中采样几个目标词负样本(如“日本”,“喝茶”等)。有了这些内容,我们的skip-gram模型就变成了一个二分类任务。对于目标词正样本,我们需要最大化它的预测概率;对于目标词负样本,我们需要最小化它的预测概率。通过这种方式,我们就可以完成计算加速。上述做法,我们称之为负采样。 模型训练过程如下: 1. 用V去查询W0,用T去查询W1,分别得到两个形状为[batch_size, embedding_size]的tensor,记为H1和H2。 2. 将这两个tensor进行点积运算,最终得到一个形状为[batch_size]的tensor $$ O = [O_i = \sum_j H_0[i, j] \times H_1[i, j]]_{i = 1}^{batch\_size}
- 使用 sigmoid 函数作用在 O 上,将上述点积的结果归一化为一个 0-1 的概率值,作为预测概率,根据标签信息 L 训练这个模型即可。
每轮采样 k 个负案例,datasets 小的时候,选 5-20 个,数据集大的时候,选 2-5 个