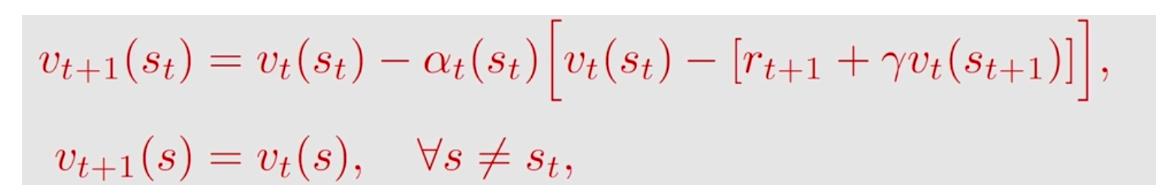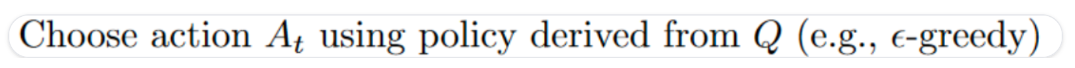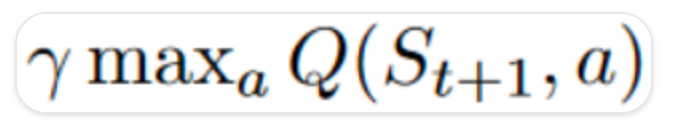# RL
强化学习(Reinforcement Learning, RL)是机器学习的一个重要分支,主要研究智能体(Agent)如何在一个环境中通过与环境交互来学习策略,以最大化某种累积奖励。强化学习的核心思想是通过试错(Trial and Error)来学习,智能体通过执行动作(Action)来影响环境,并从环境中获得反馈(Reward),进而调整其策略(Policy)以优化长期奖励。
# Math
x$$ 代表观测值,$$X $$代表随机变量 #### 概率密度函数 是描述连续型随机变量概率分布,随机变量 X 落在某一点附近的可能性密度有多大 单点概率 P(X=a)=0 真正有意义的是区间概率:随机变量 X落在区间 [a,b] 的概率通过 PDF 的积分计算:$$P(a<=X<=b)=\int_a^bf(x)dxPDF 给出了随机变量的值等于该样本值的相对可能性。$$\int_x p (x) dx=1$$, 对于连续分布
# 数学期望
\mathbb{E}[f(X)]=\int_x p(x) {\cdot} f(x)dx$$, p(x)是概率密度函数 ,对于连续分布 它表示在多次重复试验中随机变量取值的 “长期平均值”,反映了随机变量的集中趋势。 **离散型随机变量数学期望** $$E(x)=\sum_i{x_i}\cdot P(X=x_i)- 掷一枚公平骰子
- 可能取值:x_i = 1, 2, 3, 4, 5, 6
- 每个概率:$$P (X = x_i) = \frac {1}{6}$$
- 期望值:$$ E (X) = (1 \cdot \frac {1}{6}) + (2 \cdot \frac {1}{6}) + \cdots + (6 \cdot \frac {6}{1}) = \frac {21}{6} = 3.5$$
连续型 **** 随机变量
E(X) = \int_{-\infty}^{\infty} x \cdot f(x) \, dx$$(其中 f(x)是概率密度函数) - **含义**:通过积分计算随机变量在连续值域上的加权平均。 - **例子**:某区间 [a,b] 上的均匀分布 - 密度函数:$$f(x) = \frac{1}{b-a}$$(当$$ x \in [a,b]- 期望值:$$E (X) = \int_a} x \cdot \frac{1}{b-a} , dx = \frac{a+b}{2}$$
长期平均性若进行无数次独立重复试验,随机变量 (X) 的样本平均值将无限接近其期望 E (X)。例如,长期抛骰子得到的平均点数会趋近于 3.5。
# 随机抽样
从总体中公平选取样本 的方法,其核心在于:总体中的每一个个体被抽中的概率均等,且每次抽样相互独立(或满足特定抽样规则)。
# 基本要素
- 智能体(Agent):学习和决策的主体。
- 环境(Environment):智能体交互的外部世界。
- 状态(State):环境在某一时刻的描述。
- 动作(Action):智能体在某一状态下可以执行的操作。
- 奖励(Reward):智能体执行动作后从环境中获得的反馈。
- 策略(Policy):智能体在给定状态下选择动作的规则。(策略分为确定性策略 (deterministic policy) 和不确定性策略 (stochastic policy), 确定性策略只每种状态下选择的 action 是确定的即百分之百选择一种策略,而不确定性策略指某种状态下选择的 action 是不确定的,策略只是确定 action 的分布,然后在分布中进行采样来确定策略) $$\pi (a|s)=\mathbb {P}(A=a|S=s)$$
- 价值函数(Value Function):评估在某一状态下长期累积奖励的期望值。
# RL 随机性
Actions $$\mathbb {P}[A=a| S=s] = \pi (a|s)$$ , $$\pi ()$$ 是 policy 函数
state transitions $$\mathbb {P}[S’=s’|S=s,A=s]=p (s’|s)$$ , $$p ()$$ 是状态转移函数

# Glossary
| 常用词 | 说明 | 公式 | ||
|---|---|---|---|---|
| Agent | Agent 反复试验来学习做出决定,并从周围环境中获得奖励和惩罚 。 | |||
| Environment | 环境是一个模拟世界 ,Agent 可以通过与之交互来学习 | |||
| Markov Property | Agent 所采取的行动完全以当前状态为条件,独立于过去的状态和行动 。 | |||
| Observations | 对环境 / 世界状态的部分描述。 | |||
| State | 世界状态的完整描述。 | |||
| state transition | 状态转移,状态转移可以是随机的。只有环境知道,Agent 不知道会如何转移 | $$p(s’ | s,a) = \mathbb{P}(S’=s’ | S=s,A=a)$$ |
| return | 未来累计奖励,Rt 代表还未发生的奖励 | $$\sum_k=0}r_{t+k+1} $$ | ||
| Discounting return | 开始时获得的奖励更有可能发生,因为它们比长期奖励更容易预测。 | $$R(\tau)=\sum_k=0} \gamma^k r_t+k+1} R(\tau)=r_{t+1}+ {\gamma} r_{t+2}+ {\gamma} + \dots U_t=R_t+ \gamma R_t+1} + {\gamma} + \dots$$ | ||
| expected return | 最大化其累积奖励 | |||
| Discrete Actions | 有限数量的动作,例如 left、right、up 和 down。 | |||
| Continuous Actions | 有无限可能性的动作;例如,在自动驾驶汽车的情况下,驾驶场景具有发生动作的无限可能性。 | |||
| Action space | 一个环境中所有可能动作的集合 | |||
| Rewards | RL 的基本因素。告诉 Agent 所采取的作是好的还是坏的。 | $$R(\tau)=\sum_k=0}r_{t+k+1} $$ | ||
| Reward Hypothesis | RL 问题可以表述为(累积)回报的最大化。 | |||
| action value function | Q (s,a) 对于策略 π, Agent 评估在状态 S,执行动作 at 的好坏 | $$Q_{\pi}(s_t,a_t)=\mathbb{E}[U_t | S_t=a_t,A_t=a_t]$$ | |
| state value funcion | 对于固定策略 π,Vπs 评估在状态 s 下局势的优劣 | $$V_{\pi}(s)=\mathbb{E}A[Q(s,A)]$$ | ||
| optimal Action-value function | 执行 at 最大期望回报 | $$Q^*(s_t,a_t)=\max_{\pi} \mathbb{E}[U_t | S_t=s_t,At=a_t]$$ | |
| trajectory | (state,action,reward) 组合, | |||
| Episodic task | 具有起点和终点。 | |||
| Continuous task | 有起点,但没有终点。 | |||
| Exploration | 通过尝试随机动作并从环境中接收反馈 / 回报 / 奖励来探索环境 | |||
| Exploitation | 利用我们对环境的了解来获得最大的回报。 | |||
| Exploration-Exploitation Trade-Off | 平衡了想要探索环境的程度和我们想要利用我们对环境的了解的程度。 | |||
| Policy | 告诉 Agent 在给定状态的情况下要采取什么行动。 | |||
| policy network | 使用神经网络去近似 在状态 s 下执行动作 a 的概率 | $$\pi(a | s; \theta) $$ | |
| Optimal Policy | 当 Agent 按照此策略行动时,能使预期回报最大化的策略。它是通过训练习得的。其中,预期回报指在 Agent 采取行动时所期望获得的收益。 | |||
| Policy-based Methods | 一种解决 RL 问题的方法 ,在这种方法中,Policy 是直接学习的。将每个状态映射到该状态下的最佳对应行动。或者该状态下一组可能行动的概率分布。 | |||
| Value-based Methods | 解决 RL 问题的另一种方法。相反,我们不训练策略,而是训练一个价值函数,该函数将每个状态映射到处于该状态的预期值。 | |||
| Bellman equation | ||||
| Monte Carlo | ||||
| Temporal Difference | ||||
| TD target | ||||
| epsilon-greedy | ||||
| Q-learning | ||||
| Off-policy | ||||
| On-policy | ||||
| Sarsa | ||||
| DQN | ||||
| Tabular Method | 一种问题类型,其中状态空间和动作空间足够小,可以近似表示为数组或表格的价值函数。 | |||
| Deep Q-learning | 一种训练神经网络的方法,该方法根据给定的状态,近似表示在该状态下每个可能动作的不同 Q 值。 | |||
| Experience Replay | ||||
| Random sampling | ||||
| Fixed Q-Target | ||||
| Double DQN | ||||
| Actor-Critic | ||||
| policy gradient | 目标是使用梯度上升最大化参数化策略的性能,策略梯度的目标是通过调整策略来控制动作的概率分布,使得未来更频繁地采样到好的动作 | |||
| Monte Carlo Reinforce | 一种策略梯度算法,使用整个 episode 的估计回报来更新策略参数。 | |||
| rlhf | ||||
| PPO | 近端策略优化,一种通过避免策略更新过大来提高代理训练稳定性的架构 | |||
# (Value-Based) / (Policy-Based)
策略 π 是我们智能体的核心,它是根据当前状态告诉我们应该采取什么行动的函数。因此,它定义了智能体在给定时间的行为。这个策略是我们想要学习的函数,我们的目标是找到最优策略 π*,即在 Agent 根据其行动时最大化预期回报的策略。我们通过训练找到这个 π*。
基于价值的方法(Value-Based Methods)和基于策略的方法(Policy-Based Methods)是强化学习中的两类主要算法,它们使用不同的方式来处理智能体在环境中的决策问题。直接通过教导代理在当前状态下应采取何种行动 (Policy-based)。教 Agent 学习哪个状态更有价值,然后执行更有价值的动作。(value-based)
# 基于价值的方法 (Value-Based Methods):
基于价值的方法专注于寻找一个价值函数,它给出了每个状态(或状态 - 动作对)的价值,代表了从该状态(或执行该动作)开始并遵循某个策略所能获得的期望回报(expected return)。基本思想是价值函数可以指导智能体如何选择动作:在给定状态下,选择使价值最大化的动作。
- Q-Learning: Q-Learning 是典型的基于价值的方法之一。它学习一个动作价值函数(action-value function)Q,该函数输出在给定状态下执行某个动作的预期回报。智能体在每个状态下选择能够最大化 Q 值的动作。
- 价值函数表示:价值函数通常使用表格(Q 表)或参数化模型(例如,神经网络)来表示。
# 基于策略的方法 (Policy-Based Methods):
基于策略的方法不直接学习价值函数,而是直接参数化并优化策略本身。策略是从状态到动作的映射,可以是确定性 (Deterministic) 的也可以是随机性 (Stochastic) 的。通过调整策略的参数来优化策略以最大化智能体的期望回报。
- 确定性:在给定状态下,策略总是返回相同的行动。$$a=\pi (s)$$
- 随机性:输出一个动作的概率分布。$$\pi (a|s)=P [A|s]$$, 给定当前状态 s 时,动作集合上的概率分布
- 直接优化:与基于价值的方法不同,基于策略的方法直接优化策略函数。策略可以用各种函数(如神经网络)来参数化,目标是找到最佳参数集使得长期回报最大化。
- 适用性:基于策略的方法尤其适用于动作空间是高维的或连续的问题,因为它们可以学习在任何时刻给出具体动作的策略。
- 梯度估算:通常通过策略梯度定理来估算策略的梯度,并通过梯度上升(或下降)来优化策略。
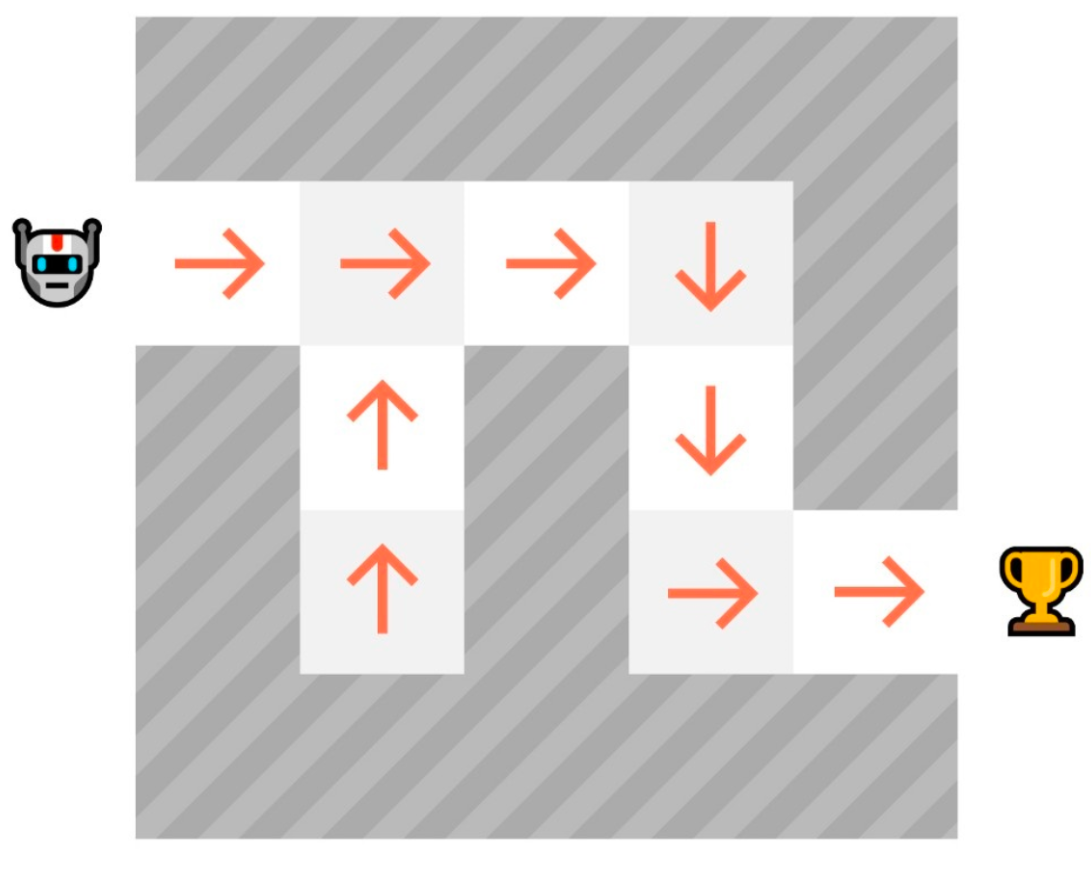
# 对应算法
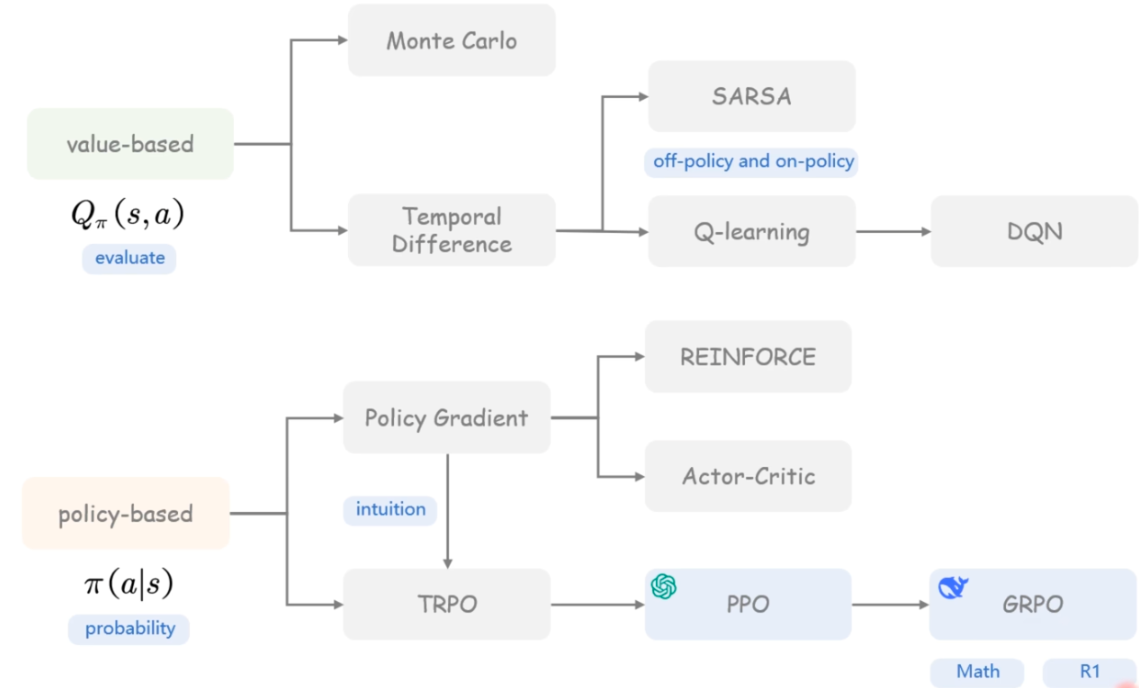
常见的强化学习算法包括:
- Q-learning:基于值的算法,学习每个状态 - 动作对的值。
- 深度 Q 网络(DQN):结合深度学习,使用神经网络近似 Q 函数。
- 策略梯度 **(Policy Gradient)**:直接优化策略的参数,而不是值函数。
# Q-learning
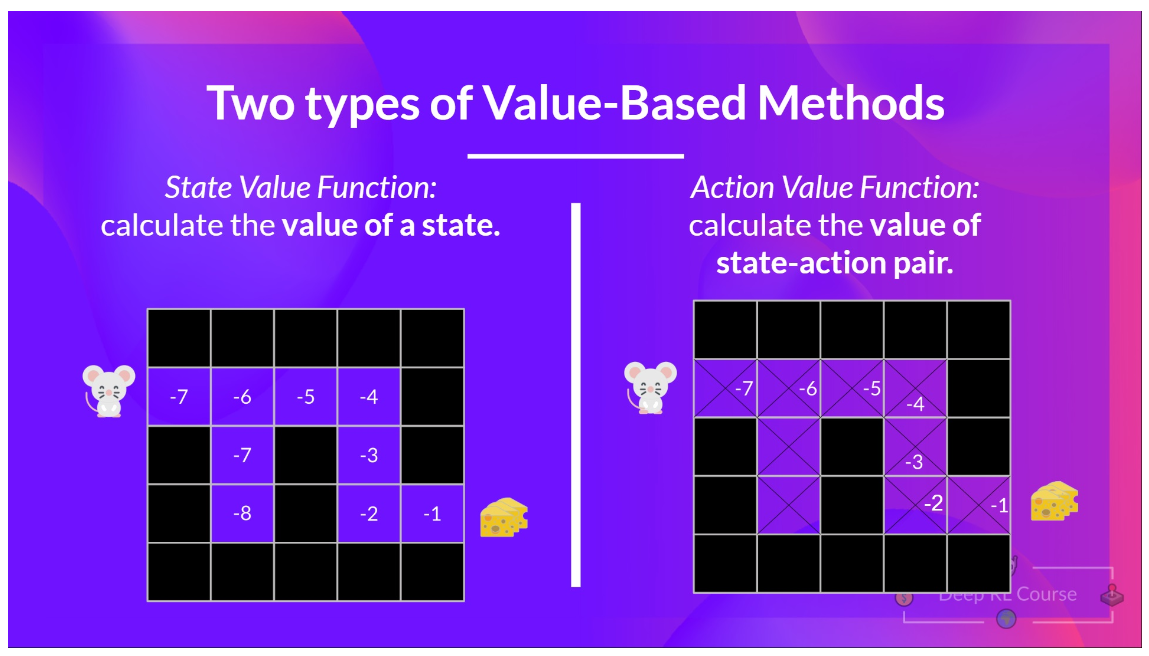
在基于价值的方法中,我们有两种策略
state-value function - 对于每个状态,状态值函数是指智能体从该状态开始并遵循策略直到结束时的预期回报。
action-value function - 与状态值函数不同,动作值函数计算智能体从该状态开始,采取该动作,然后永远遵循策略后的预期回报。
# Bellman equation
这相当于 V(St) = 立即奖励 Rt+1 + 下一个状态的折扣价值 γ∗V(St+1)
V(St+1) 的价值 = 立即奖励 Rt+2 + 下一个状态的折扣价值 ( gamma∗V(St+2) )。
以此类推
贝尔曼方程的思路是,我们不再将每个价值计算为预期收益的总和,而是将价值计算为立即奖励 + 后续状态的折扣价值之和。
# Monte Carlo
蒙特卡洛会等到 episode 结束,计算 Gt (回报)并将其用作更新 V(St) 的目标。因此,它需要在交互完整个 episode 后才能更新我们的价值函数。
Monte Carlo approach
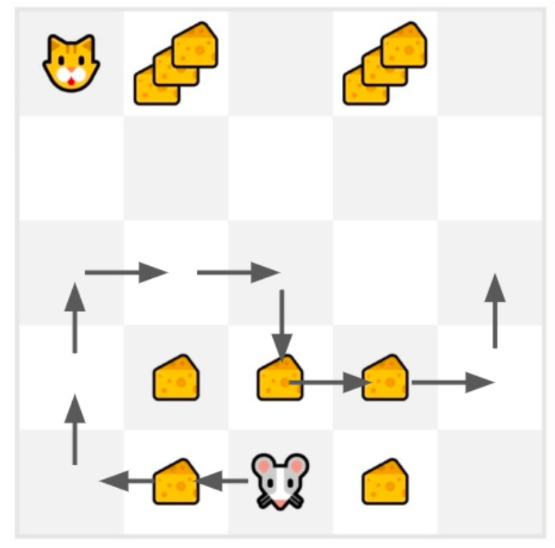
Gt=0
Gt=Rt+1+Rt+2+Rt+3…(for simplicity, we don’t discount the rewards)
G0=R1+R2+R3…
G0=1+0+0+0+0+0+1+1+0+0
G0=3
计算新的 V (s0)
V(S0)=V(S0)+lr∗[G0—V(S0)]
V(S0)=0+0.1∗[3–0]
V(S0)=0.3
# Temporal Difference
时序差分只等待有一次交互 St+1 来形成 TD 目标,并使用 Rt+1 和 γ∗V (St+1) 更新 V (St) 。
TD 的思想是在每一步更新 V (St)。
但由于我们没有经历整个 episode,我们没有 Gt (预期回报)。我们通过加上 Rt+1 和下一个状态的 discounted value 来估计 Gt。
预测值 $$q=Q (w)$$ , target 真实值 y
完成全部步骤再更新
Loss $$L=\frac{1}{2}(q-y)^2$$
gradient $$ \frac{\partial L}{\partial \boldsymbol{w}} = \frac{\partial q}{\partial \boldsymbol{w}} \cdot \frac{\partial L}{\partial q} = (q - y) \cdot \frac{\partial Q(\boldsymbol{w})}{\partial \boldsymbol{w}} $$
gradient descent $$W_{t+1}=W_t - \alpha \cdot \frac{\partial{L}}{\partial{w}}|_{w=w_t}$$
TD learning - 完成一定步骤后就更新
TD target = estimate + actual
模型估计 Q (w)
Loss $$L=\frac{1}{2}(Q(w)-y)^2$$ Q(w)-y TD-error
# TD learning Approach
这被称为 bootstrapping。因为 TD 的部分更新基于现有的估计 V (St+1) 而不是完整的样本 Gt 。

假设 $$\alpha=0.1,\gamma=1$$, 采取 Action,向左移动,获得奶酪, $$R_{t+1}=1$$,更新 V (S0)
New V(S0)=V(S0)+lr∗[R1+γ∗V(S1)−V(S0)]
NewV(S0)=0+0.1∗[1+1∗0–0]
NewV(S0)=0.1
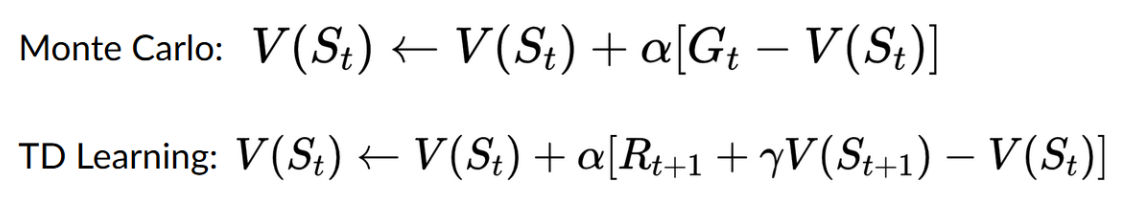
# Q-learning
Q-Learning 是一种 Off-policy 的基于价值的方法,它使用时序差分方法来训练其动作价值函数:
基于价值的方法:通过训练一个价值或动作价值函数来间接找到最优策略,该函数将告诉我们每个状态或每个状态 - 动作对的价值。
TD 方法:在每个步骤中更新其动作值函数,而不是在 episode 结束时更新。
Q-Learning 是我们用来训练 Q 函数的算法,Q 函数是一个动作值函数,它决定了处于特定状态并采取特定动作时的价值。
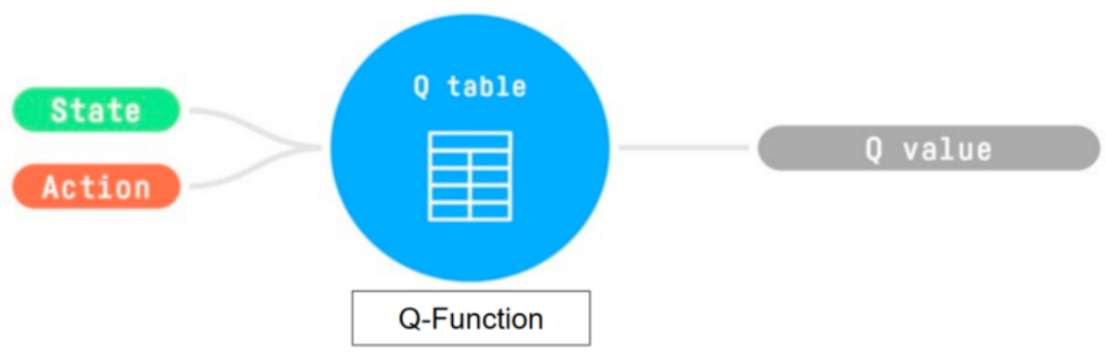
我们的 Q 函数由一个 Q 表编码,Q 表中的每个单元格对应一个状态 - 动作对的价值。将这个 Q 表视为我们 Q 函数的记忆

Q 表被初始化。这就是为什么所有值都等于 0。这个表包含了每个状态和动作对应的状体 - 动作值。对于这个简单的例子,状态仅由老鼠的位置定义。因此,我们的 Q 表有 2*3 行,每一行对应老鼠的一个可能位置。
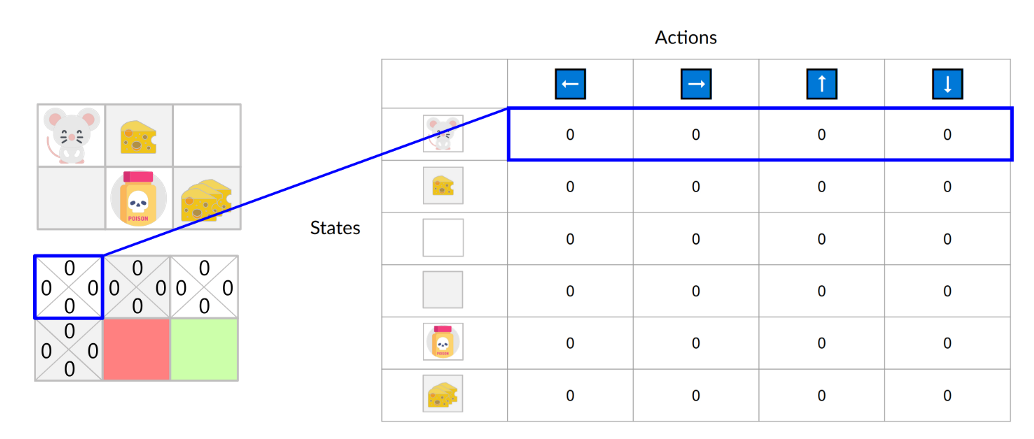
初始状态向上移动的状体 - 动作值是 0:

Q 函数使用一个 Q 表,其中包含每个状体 - 动作对的价值。给定一个状态和动作,我们的 Q 函数会在其 Q 表中查找并输出该值。
# Q-learning step
1、训练一个 Q 函数(一个动作值函数),其内部是一个包含所有状态 - 动作对值的 Q 表。
2、给定一个状态和动作,我们的 Q 函数会在其 Q 表中搜索相应的值。
3、当训练完成后,我们得到一个最优的 Q 函数,这意味着我们得到了一个最优的 Q 表。
4、如果我们有一个最优的 Q 函数,我们也就有一个最优策略,因为我们知道在每个状态下采取的最佳行动。
\pi^*(s)=\argmax_a Q^*(s,a)$$ 找到一个最优值函数会得到一个最优策略 一开始,我们的 Q 表是无用的,因为它为每个状态-动作对给出任意值(通常我们将 Q 表初始化为 0)。随着智能体探索环境并更新 Q 表,它将给我们提供越来越接近最优策略的近似值。 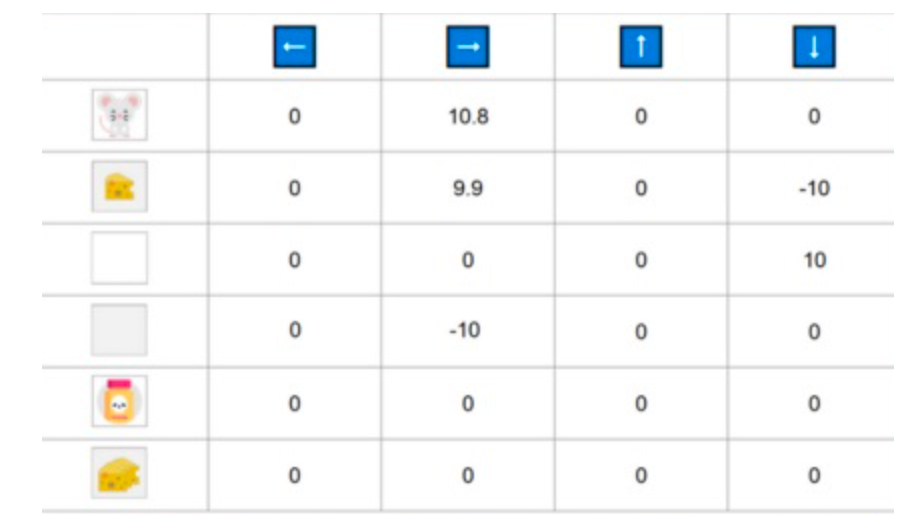 Q-learning algorithm **1、初始化Q表,**通常情况下,我们用 0 来初始化这些值。 **2、使用 epsilon-greedy 策略选择一个动作**。epsilon-贪婪策略是一种exploration/exploitation权衡的策略。 > 初始值为ɛ = 1.0,以概率 1 — ɛ:我们进行exploitation ,即我们的智能体选择具有最高状态-动作对值的动作)。 > > 以概率ɛ:我们进行探索(尝试随机动作)。 在训练开始时,由于ɛ值非常高,进行探索的概率将非常大,因此大部分时间我们会进行探索。但随着训练的进行,我们的 Q 表在估计方面会越来越好,我们会逐步降低 epsilon 值,因为我们需要的探索越来越少,而exploitation得越来越多。 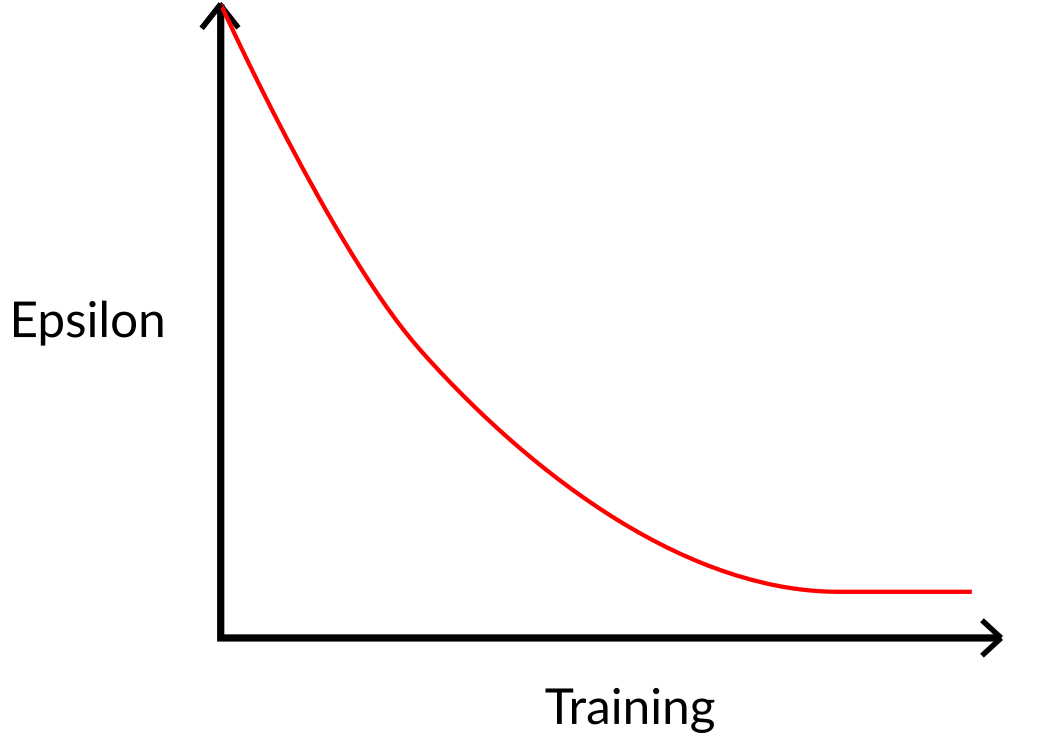 **步骤 3:执行动作 At,获得奖励 Rt+1 和下一个状态 St+1** **步骤 4:更新 Q(St, At),更新Q(St, At)的公式如下** $$Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \left[ R_{t+1} + \gamma \max_a Q(S_{t+1}, a) - Q(S_t, A_t) \right]- Q(S_t, A_t)$$ :当前状态 S_t下执行动作A_t 的旧 Q 值
- \max_a Q(S_{t+1}, a)$$:下一状态 S_{t+1} 下所有可能动作的最大 Q 值
我们采取动作 At 后获得奖励 Rt+1。为了获得下一个状态的最佳状态 - 动作对值,我们使用贪婪策略选择下一个最佳动作。这不是一个 epsilon - 贪婪策略,它将始终选择具有最高状态 - 动作值的行为。
当这个 Q 值的更新完成后,我们进入一个新的状态,并再次使用 epsilon - 贪婪策略选择我们的动作。
# off-policy / on-policy
off-policy: 使用不同的策略进行行动(推理)和更新(训练)
在 Q-Learning 中,epsilon-greedy 策略(行动策略)与用于选择最佳下一状态动作值以更新我们的 Q 值的贪婪策略(更新策略)是不同的。
Q-learning action policy
Q-learning updating policy
On-policy*😗 using the same policy for acting and updating.
sarsa 中,Action 和 updating policy 都是使用 $$\epsilon-greedy$$ 的。 Sarsa 是另一种基于值的算法中
# Deep Q-learning
Q-Learning 是一种表格方法。当状态空间和动作空间不够小以至于无法高效地用数组和表格表示时,这就会成为问题。换句话说:它不具备可扩展性。Q-Learning 在小状态空间环境中表现良好
在大型状态空间环境中,生成和更新 Q 表会变得低效。深度 Q 学习不是使用 Q 表,而是使用一个神经网络,该网络接收一个状态,并根据该状态近似每个动作的 Q 值。
在这种情况下,最好的想法是使用参数化的 Q 函数 $$Q_{\theta}(s,a)$$ 来近似 Q 值。这个神经网络将根据状态,近似该状态下每个可能动作的不同 Q 值。而这正是深度 Q 学习所做的。
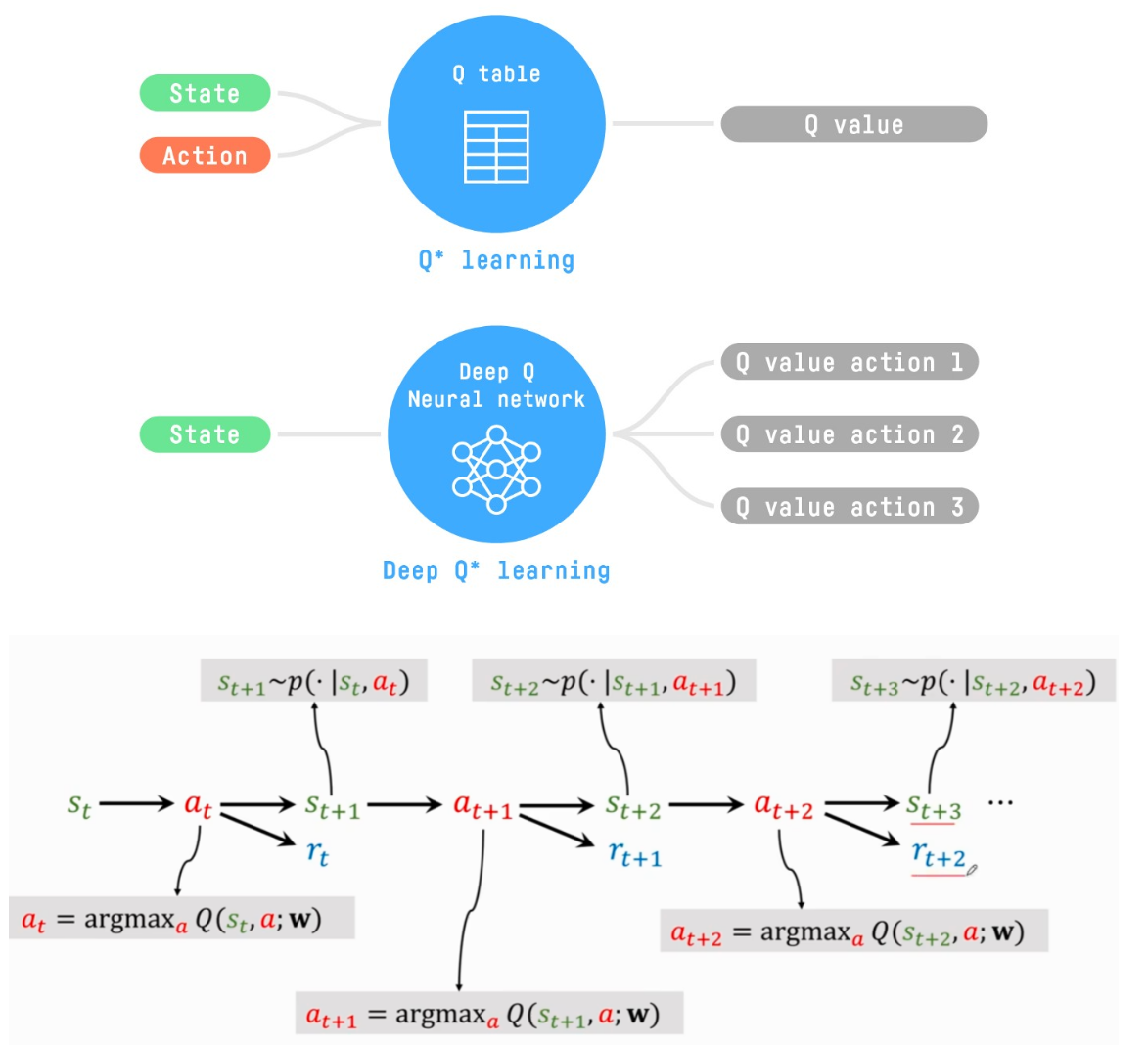
# Deep Q Algorithm
与 Q-learning 不同之处在于,在训练阶段,我们不是像 Q 学习那样直接更新状态 - 动作对的 Q 值
在深度 Q 学习中,我们创建一个损失函数,该函数比较我们的 Q 值预测和 Q 目标,并使用梯度下降来更新深度 Q 网络的权重,以更好地近似我们的 Q 值。
Q(s_t, a_t; \boldsymbol{w}) \approx r_t + \gamma \cdot Q(s_{t + 1}, a_{t + 1}; \boldsymbol{w}) $$ rt是real value ,$$ Q(s_t, a_t; \boldsymbol{w})$$ 是模型估计 **Q-target** $$ y_j = r_j + \gamma \max_{a'} \hat{Q} \left( \phi_{j+1}, a' ; \theta^- \right)- \max_{a'} \hat{Q}(\phi_{j+1}, a' ; \theta^-)$$ :基于目标网络(参数 $$\theta^-$$),对下一状态 $$ \phi_{j+1} $$ 下所有可能动作a',取 Q 值最大的那个,代表未来最优收益的估计。
Q-loss

gradient descent
深度 Q 学习训练算法有两个阶段:
采样:我们执行动作并将观察到的经验元组存储在 replay memory.
训练:随机选择一小批元组,并使用梯度下降更新步骤从这批元组中学习。

深度 Q-Learning 训练可能会出现不稳定性,主要是因为结合了非线性 Q 值函数(神经网络)和自举(当我们用现有估计更新目标而不是实际完整回报时)。
为了稳定训练,实现了三种不同的解决方案:
- 经验回放 (Experience Replay) 以更有效地利用经验。
- 固定 Q-Target 以稳定训练。
- 双深度 (Double Deep Q-Learning) Q 学习,以处理 Q 值过估计的问题。
# Experience Replay
深度 Q 学习的经验回放有两个功能:
更有效地利用训练过程中的经验。通常,在线强化学习中,智能体与环境交互,获取经验(状态、动作、奖励和下一状态),从中学习(更新神经网络),然后丢弃这些经验。这并不高效。
经验回放通过更有效地利用训练经验来提供帮助。我们使用一个经验回放缓冲区,它保存我们可以在训练期间重复使用的经验样本
这使得智能体能够多次从相同经验中学习。

初始化一个容量为 N(N 是一个可以定义的超参数)的回放记忆缓冲区 D。然后我们将经验存储在记忆中,并在训练阶段从记忆中采样一批经验来为深度 Q 网络提供输入。

避免遗忘先前经验(即灾难性干扰,或灾难性遗忘),并减少经验之间的相关性。
灾难性遗忘:当我们向神经网络提供连续的经验样本时,会出现的问题是其倾向于在获得新经验时忘记先前经验。例如,如果智能体在第一关然后进入第二关(后者不同),它可能会忘记如何在第一关中行为和玩耍。
创建一个经验回放缓冲区,在与环境交互时存储经验元组,然后从中采样一小批元组。这防止了网络只学习它刚刚做的事情。
通过随机采样经验,我们消除了观察序列中的相关性,并避免了动作值发生灾难性振荡或发散。
# fixed Q-target
当我们想要计算 TD 误差时,我们计算 TD 目标与 Q 的估计值之间的差异。
我们使用相同的参数(权重)来估计 TD 目标和 Q 值。在训练的每一步,我们的 Q 值和目标值都会发生偏移。我们似乎在接近目标,但目标也在移动。这可能导致训练过程中出现显著的振荡。
使用一个具有固定参数的独立网络来估计 TD 目标,每隔 C 步从我们的深度 Q 网络中复制参数来更新目标网络。

# Double DQN
双深度 Q-learning neural netowks, 这种方法解决了 Q 值高估的问题。
高估原因:自举,最大化
在计算 Q 目标时,我们使用两个网络来将动作选择与目标 Q 值生成解耦。
使用我们的 DQN 网络来选择为下一个状态采取的最佳动作
使用我们的 Target network 来计算在下一个状态下采取该行动的目标 Q 值。
# Policy gradient
强化学习的主要目标是找到能最大化预期累积奖励的最优策略 π∗ 。因为强化学习基于奖励假设:所有目标都可以描述为预期累积奖励的最大化。
在基于策略的方法中,我们直接学习近似 π∗ ,而无需学习价值函数。policy-based methods 思想是对策略进行参数化。例如,使用神经网络 πθ ,该策略将输出一个动作的概率分布
基于策略方法,我们可以直接优化我们的策略 πθ 以输出导致最佳累积回报的动作概率分布 πθ(a∣s) 。为此,我们定义了一个目标函数 J (θ),即预期累积奖励,并且我们希望找到最大化这个目标函数的值 θ。
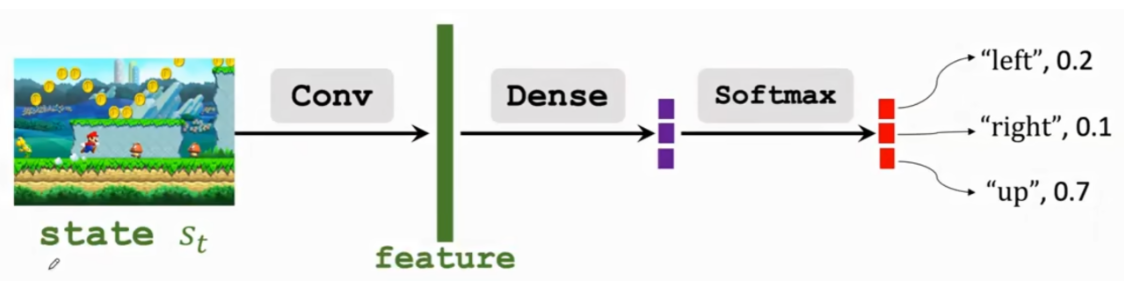
\pi(a|s)$$ 输入状态s,输出动作的概率值 policy network $$\pi(a|s,\theta)$$ 满足性质$$\sum_{a\in A} \pi(a|s;\theta)=1$$, 即概率加和=1 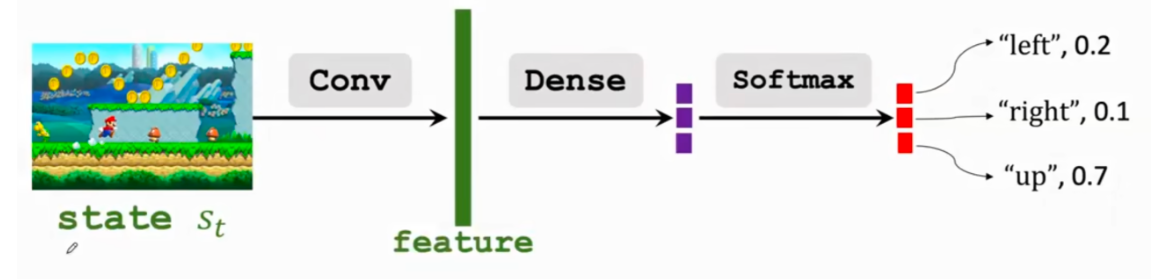 Action Value function $$Q_{\pi}(s_t,a)$$ 在st状态执行at动作的好坏 state value function $$V_{\pi}(S_t)=\mathbb{E}_A[Q_{\pi}(s_t,A)]=\sum_a \pi(a|s_t) \cdot Q_{\pi}(s_t,a)$$ 评价在策略$$\pi$$ 好坏 对于policy network,用神经网络近似 $$V(s_t;\theta)=\sum_a \pi(a|s_t;\theta) \cdot Q_{\pi}(s_t,a)$$ ,$$\theta $$是神经网络参数 因此policy based learning 目标是最大化 $$J(\theta)=\mathbb{E}_S[V(S;\theta)]使用梯度上升 来优化 $$\theta$$, $$\theta \leftarrow \theta +\beta \cdot \frac {\partial V (s;\theta)}{\partial \theta}$$
policy gradient $$\frac{\partial V(s;\theta)}{\partial \theta}$$ $$= \mathbb{E}{A \sim \pi (\cdot | s; \theta)} \left[ \frac{\partial \log \pi(A \mid s; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}} \cdot Q\pi (s, A) \right]$$ 对于连续变量适用
\frac{\partial V(s; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}} = \sum_{a} \frac{\partial \pi(a \mid s; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}} \cdot Q_{\pi}(s, a)$$ 对于离散动作适用 对$$ \mathbb{E}_{A \sim \pi (\cdot | s; \theta)} \left[ \frac{\partial \log \pi(A \mid s; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}} \cdot Q_\pi(s, A) \right]$$ 做蒙特卡洛近似,根据$$\pi$$抽样 得到$$\hat{a}计算 $$g (\hat {a},\theta)=\left [ \frac {\partial \log \pi (A \mid s; \boldsymbol {\theta})}{\partial \boldsymbol {\theta}} \cdot Q_\pi (s, A) \right]$$,$$g (\hat {a},\theta)$$ 是 $$\frac {\partial V (s;\theta)}{\partial \theta}$$ 的无偏估计,用 $$g (\hat {a},\theta)$$ 近似策略梯度
计算 $$Q_{\pi}(s,a)$$ 方式 1 Reinforce 玩完证据游戏得到 (ST,aT,rT) 用 ut 近似
方式 2: actor-critic
# 策略梯度
是基于策略方法的子类。在基于策略方法中,优化通常是 in-policy 的,因为每次更新时,我们只使用由我们最新版本的 πθ 收集的数据 (trajectories)
在基于策略的方法中,我们直接搜索最优策略。我们可以通过使用爬山、模拟退火或进化策略等技术来间接优化参数 θ,通过最大化目标函数的局部近似值。
在策略梯度方法中,因为它是一种基于策略方法的子类,我们直接搜索最优策略。但我们通过在目标函数 J (θ) 的表现上执行梯度上升来直接优化参数 θ 。
# policy gradient advantage
- 我们可以直接估计策略,而无需存储额外的数据(action value)。
- 策略梯度方法可以学习随机策略,而值函数则不能。
- 不需要手动实现 exploration/exploitation trade-off。由于我们输出的是动作的概率分布,智能体可以在不一直采取相同轨迹的情况下探索状态空间。
- 解决了感知别名 (perceptual aliasing) 问题。感知别名是指两个状态看似(或实际)相同,但需要采取不同动作的情况。
perceptual aliasing
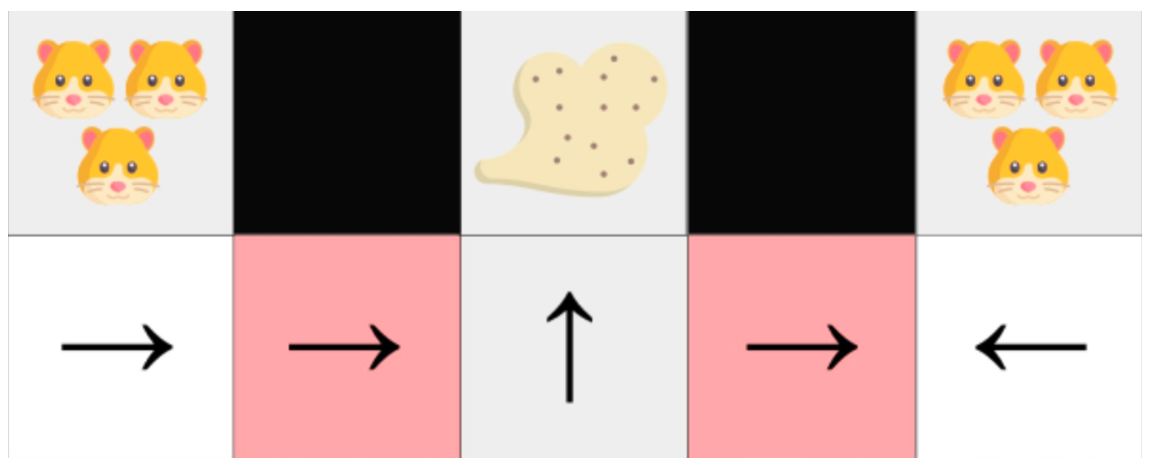
这两个红色状态是别名状态,因为智能体对每个状态感知到上墙和下墙。
在确定性策略下,策略在红色状态下会一直向右移动或一直向左移动。无论哪种情况都会导致我们的智能体卡住,并且永远不会吸走灰尘。
一个最优随机策略在红色状态下会随机向左或向右移动。因此,它不会卡住,并且以高概率达到目标状态。
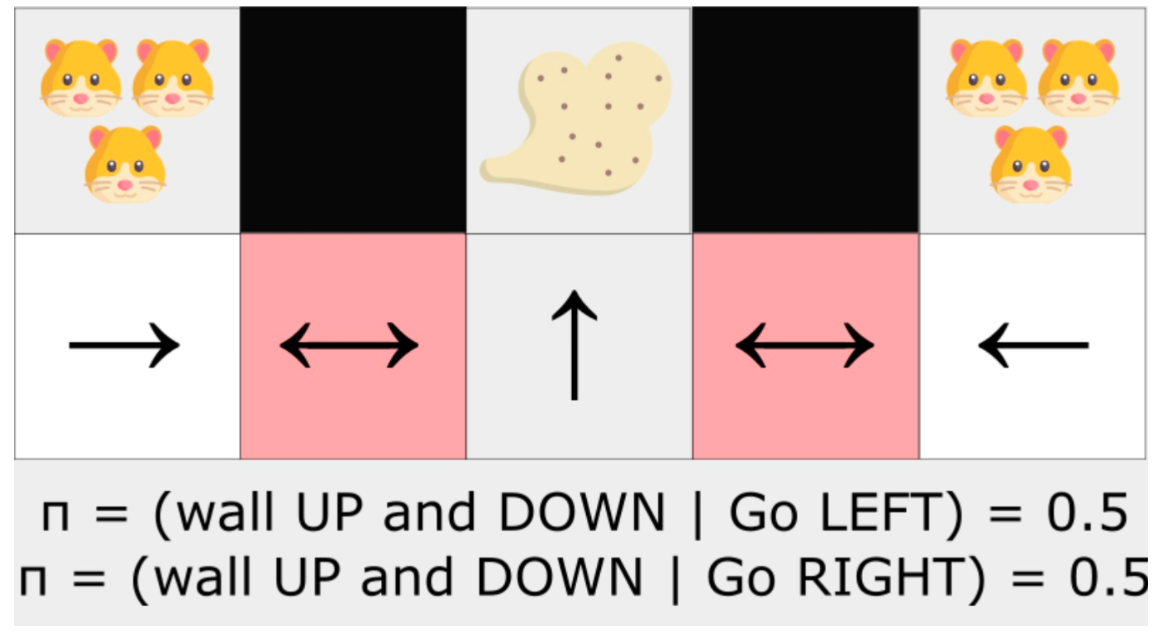
- 策略梯度方法在高维动作空间和连续动作空间中更有效。使用策略梯度方法时,我们输出的是关于动作的概率分布。
在策略梯度方法中,随机策略动作偏好(采取动作的概率)会随着时间的推移而平滑变化。
- 策略梯度方法具有更好的收敛特性
# policy gradient disadvantage
- 通常,策略梯度方法会收敛到一个局部最优解,而不是全局最优解。
- 策略梯度进展缓慢,逐步进行:训练可能需要更长时间(效率低下)。
- 策略梯度可能具有高方差。
# policy gradient algorithm
让代理在一段 episode 中互动。如果我们赢得了这段 episode,我们认为所采取的每个行动都是好的,并且必须在将来更多地 sample,因为它们导致了胜利。因此对于每个状态 - 动作对,我们想要增加 P (a∣s) :在该状态下采取该动作的概率。如果我们输了,就减少它。
# stochastic policy
给定一个状态的策略会输出该状态下各个动作的概率分布。
其中 $$\pi_\theta (a_t|s_t)$$ 是智能体在给定策略下,从状态 s_t 中选择动作 a_t 的概率。
为了衡量 policy,定义了 objective function $$J (\theta)$$
# objective function
目标函数给出了在给定 trajectory(不考虑奖励的状态动作序列,与 episode 不同)下智能体的性能,并输出预期的累积奖励。
J(\theta)=\mathbb{E}_{\tau \sim \pi}[R(\tau)]$$,$$R(\tau) $$指累计Reward,$$\tau$$是状态和动作的序列,$$\tau \sim \pi$$表示轨迹 $$\tau$$ 是从策略 $$\pi$$生成的分布中采样得到的。 所有可能的 $$\tau$$ 会形成一个由 $$\pi$$决定的概率分布。 $$\mathbb{E}_{\tau \sim \pi}$$:表示对所有服从策略 $$\pi$$的轨迹 $$\tau$$ 求期望。 预期回报是所有可能的回报 R(τ)可以取的值的权重平均值,权重由回报$$R(\tau)$$所有可能取值的$$P(\tau;\theta)$$给出 $$J(\theta)=\sum_{\tau}P(\tau;\theta)R(\tau)R(τ) : 任意轨迹的回报。为了获取此数量并用它来计算预期回报,我们需要将其乘以每个可能轨迹的概率。
P(τ;θ) : 每个可能轨迹的概率 τ (该概率取决于 θ ,因为它定义了用于选择轨迹动作的策略,而该动作会对所访问的状态产生影响)。
J(θ) :预期回报,我们通过对所有轨迹求和来计算,即在 θ 的情况下采取该轨迹的概率乘以该轨迹的回报。

我们通过对所有轨迹求和来计算期望回报 $$ J (\theta)$$,求和内容为:在给定参数 $$\theta$$ 的情况下采取该轨迹的概率,以及该轨迹的回报。
轨迹的概率(依赖于 $$\theta$$,因 $$\theta$$ 定义了用于选择该轨迹动作的策略,而策略会影响所访问的状态)
轨迹的累积回报
πθ(at∣st) 是在策略下,智能体从状态 st 选择动作 at 的概率。,P (st+1|st,at) 是状态分布,也称为动态环境

Goal:find weights $$\theta$$ maximize the objective function
# gradient ascent
策略梯度是一个优化问题:我们想要找到能够最大化目标函数 J (θ) 的 θ 值,因此需要使用梯度上升 。它给出了 J (θ) 最陡峭增长的方向。
梯度上升更新步骤 $$ \theta \leftarrow \theta + \alpha * \nabla_{\theta} J (\theta)$$
以反复应用此更新,使 θ 收敛到最大化 J (θ) 的值。
计算 J (θ) 的导数存在两个问题:
- 我们无法计算目标函数的真实梯度,因为它需要计算每条可能轨迹的概率,而这在计算上非常耗时。因此,我们想用基于样本的估计值(收集一些轨迹)来计算梯度估计值 。
- 为了微分这个目标函数,我们需要微分状态分布,即马尔可夫决策过程动力学。它与环境相关。它给出了在给定当前状态和 Agent 采取的行动的情况下,环境进入下一个状态的概率。问题在于我们无法微分它,因为我们可能不知道它。
使用策略梯度定理,将目标函数变为可微分
# Monte Carlo Reinforce
强化算法(也称为蒙特卡洛策略梯度)是一种策略梯度算法,它使用整个 episode 估计回报来更新策略参数 θ
1、使用策略 $$\pi_{\theta}$$ 收集一个 episode $$\tau$$
2、使用 episode 来估计梯度 $$\hat {g}=\nabla_{\theta} J (\theta)$$
3、更新策略权重 $$\theta \leftarrow \theta + \alpha \hat {g}$$

- 梯度的估计(假设我们仅用一条轨迹来估计梯度 )
- 在我们的策略下,智能体从状态 s_t 中选择动作 a_t 的概率
- 累积回报 (即 $$R (\tau)$$,一条轨迹 $$\tau$$ 从头到尾获得的总奖励,体现该轨迹的价值 ),如果回报很高,它将提高(状态,动作)组合的概率 。
- 使从状态 s_t 中选择动作 a_t 的(对数)概率最速上快的方向
也可以收集多个 episodes(trajectories) 来估计梯度:
# Advantage Actor-Critic
使用蒙特卡洛采样来估计回报(我们使用一个完整的 episode 来计算回报),策略梯度估计存在显著的方差。蒙特卡洛方差 会导致训练速度变慢,因为我们需要大量样本来缓解它 。
Actor-Critic 方法 ,这是一种结合了基于价值和基于策略的方法的混合架构,它可以通过减少方差来稳定训练:
Actor 控制 Agent 行为 (Policy-Based method)
Critic 衡量所采取行动的好坏的(基于价值的方法)
# variance in Reinforce
Reinforce 中我们希望按照回报率的高低成比例地增加轨迹中动作的概率 。如果回报很高 ,我们就会提高 (状态,动作)组合的概率。
这种方法的优点在于它没有偏差。由于我们没有估算收益 ,因此我们只使用获得的真实收益。
鉴于环境的随机性(即一个 episode 中的随机事件)和策略的随机性, 不同的轨迹可能导致不同的回报,从而产生较大的方差 。因此,相同的起始状态可能导致截然不同的回报。
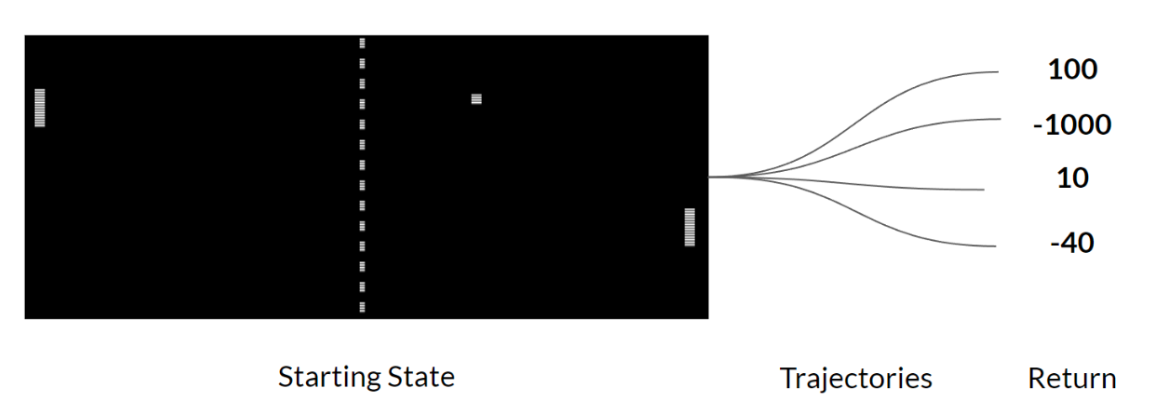
解决方案是通过使用大量 trajectories 来减轻方差,希望任何一条 trajectory 中引入的方差总体上都会减少,并提供对回报的 “真实” 估计。
state value function $$V_{\pi}(s)=\sum_a \pi(a|s) \cdot Q_{\pi}(s,a)$$
用两个神经网络近似 $$\pi (a|s) \cdot Q_{\pi}(s,a)$$
\pi(a|s;\theta) 近似 \pi(a|s) - actor$$ $$和 q(s,a;W) 近似 Q_{\pi}(s,a) - critic
policy network - actor
Update policy network$$ \pi(a \mid s; \boldsymbol{\theta}) $$ to increase the state-value $$V(s; \boldsymbol{\theta}, \boldsymbol{w}) $$
用 policy gradient 更新 policy network
value network - critic
Update value network $$q(s, a; \boldsymbol{w}) $$to better estimate the return.
用 TD 更新 value network
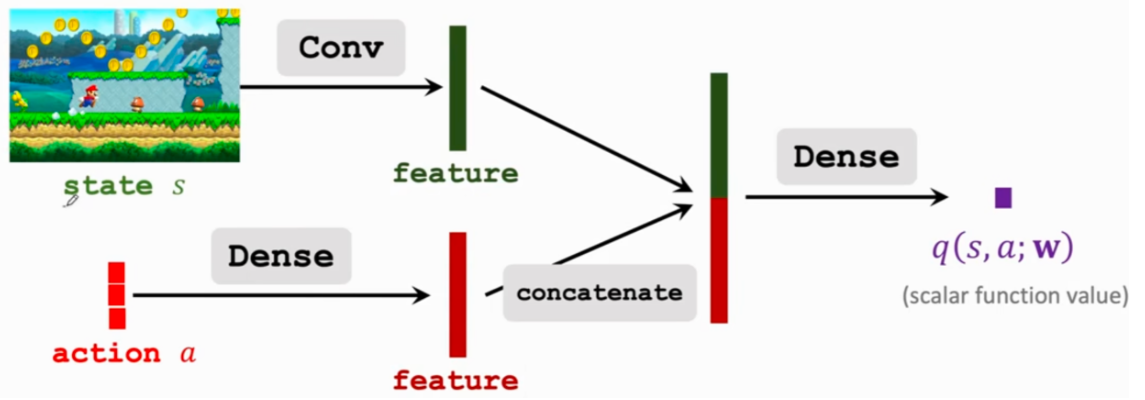
Observe the state s_t Randomly sample action a_t according to $$ \pi(\cdot \mid s_t; \theta_t) $$. Perform a_t and observe new state s_{t + 1} and reward r_t Update w (in value network) using temporal difference (TD). Update $$\theta$$ (in policy network) using policy gradient.
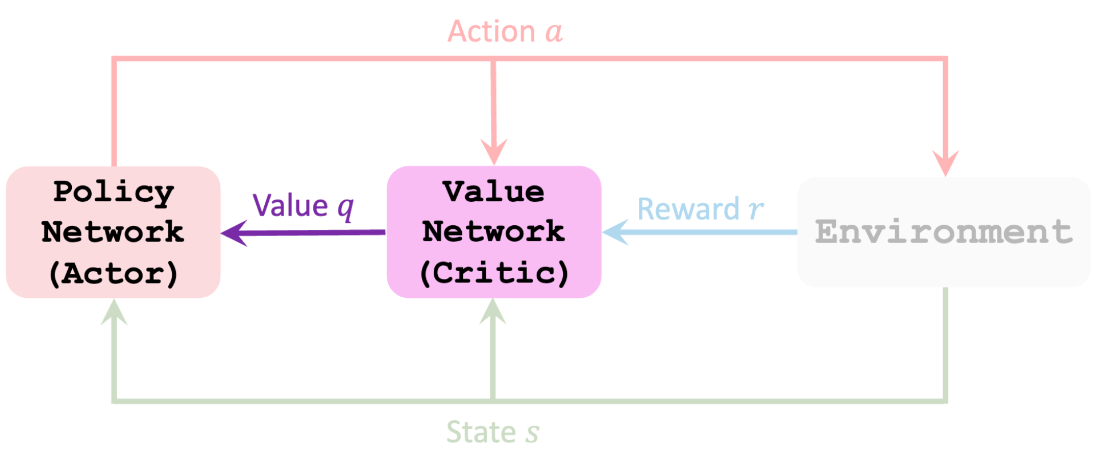
训练接受后 q 就不会使用了
# A2C
我们学习两个函数近似值:
- Actor 控制我们的 Agent 如何行动的策略 : πθ(s)
- Critic 通过衡量所采取的行动来协助策略更新的价值函数 :$$\hat {q}_w (s,a)$$
- 在每个时间步 t,我们得到当前状态𝑆 𝑡 , 从环境中获取信息并将其作为输入通过我们的 Actor 和 Critic 传递 。
- 我们的策略获取状态并输出动作 𝐴 𝑡
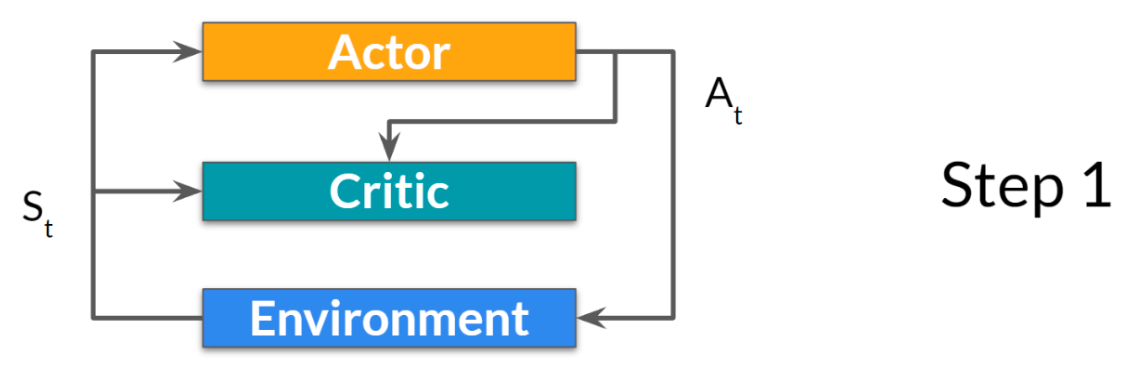
- critic 也将该动作 At 作为输入,并使用𝑆 𝑡 t 和𝐴 𝑡, 计算在该状态下采取该行动的价值:Q 值 。
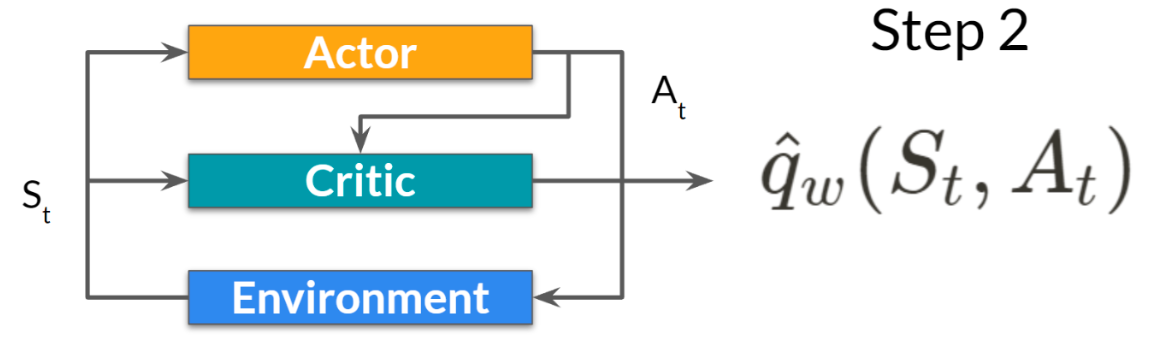
- 行动𝐴 𝑡在环境中执行的输出是一个新的状态𝑆 𝑡 + 1 和奖励𝑅 𝑡 + 1
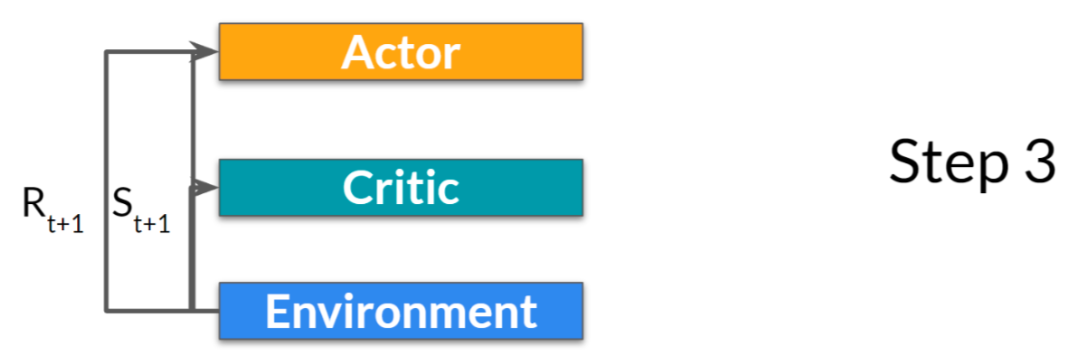
- Actor 使用 Q 值更新其策略参数。

- 由于其更新后的参数,Actor 在给定新状态 S_{t+1} 的情况下,生成在 A_{t+1} 处要采取的下一个动作。
- critic 会更新其价值参数。
# Advantage in Actor-Critic
即在某个状态下采取该动作相对于该状态的平均值如何更优 。它就是从状态动作对中减去该状态的平均值:
Advanced function $$A (s,a)=Q (s,a)-V (s)$$, V (s) 是该状态下平均值
这个函数计算了如果我们在该状态下采取这个行动,我们获得的额外奖励与我们在该状态下获得的平均奖励相比 。
额外的奖励是超出该状态的预期值的奖励。
- 如果 A (s,a) > 0:我们的梯度被推向那个方向 。
- 如果 A (s,a)< 0(我们的行动比该状态的平均值差), 我们的梯度就会被推向相反的方向 。
我们可以使用 TD 误差作为优势函数的良好估计量。

# PPO
通过避免策略更新幅度过大来提高我们 Agent 的训练稳定性。我们使用一个比率来表示当前策略与旧策略之间的差异,并将该比率限制在特定范围 [1−ϵ,1+ϵ] 内。
训练期间较小的策略更新更有可能收敛到最优解决方案。更新幅度过大,可能会导致 “跌入悬崖”(得到糟糕的政策) ,并且需要很长时间甚至没有恢复的可能。使用 PPO,我们会保守地更新策略 。为此,我们需要通过计算当前策略与先前策略之间的比率来衡量当前策略相对于先前策略的变化程度。消除了当前策略与先前策略偏离过远的诱因
Clipped surrogate objective function 该函数将使用裁剪操作把策略变化限制在一个较小的范围内。
ratio function:$$r_t (\theta)$$, $$ r_t (\theta) = \frac {\pi_\theta (a_t|s_t)}{\pi_{\theta_{\text {old}}}(a_t|s_t)} $$ 它是在当前策略下于状态 s_t 采取行动 a_t 的概率,除以前一策略下同样的概率。
rt (θ) 表示当前策略与旧策略的概率比:
- 如果 $$r_t (\theta)>1$$,那么在当前策略下,状态 s_t 处采取行动 a_t 的可能性比旧策略下更大。
- rt(θ) 介于 0 和 1 之间,该动作对于当前策略的可能性比旧策略更小
概率比率是估计旧策略和当前策略之间差异的简单方法。
unclipped part 该比率可以替代我们在策略目标函数中使用的对数概率。这为我们提供了新目标函数的左侧部分:将比率乘以优势。
如果没有约束,若所采取的行动在当前策略中的可能性远大于在之前的策略中,这将导致显著的策略梯度步长,因此导致过度的策略更新。
clipped Part
我们需要通过惩罚那些导致比率远离 1 的变化,来约束这个目标函数。在 Paper 中,取值范围额从 0.8-1.2。通过裁剪比率,我们确保不会有过大的策略更新,因为当前策略不能与旧策略过于不同。
两种约束方式
- TRPO(信赖域策略优化算法)使用目标函数外部的 KL 散度约束来限制策略更新。
- 近端策略优化算法(PPO) 通过
裁剪代理目标函数直接在目标函数中裁剪概率比。
c1 和 c2 是系数,控制价值损失和熵正则项的权重,需手动或自动调参(如 c1=0.5, c2=0.01 )。
平方误差价值损失:$$(V_\theta(s_t) - V_\text{targ}})} $$ 做 MSE 损失,让价值估计更准。
添加熵奖励以确保充分探索 衡量策略随机性,加熵项鼓励智能体探索新状态,避免过早收敛到次优策略。

AlphaGo
1、IL
2、训练策略网络
3、训练价值网络
monte carlo tree search
selection
expansion
evaluation
backup
# DQN
# 经验回放
1、重复利用经验
2、打散序列 消除相关性
优先经验回放
If a transition has a high TD error, it will be given high priority.

# TRPO/GRPO
# paper
https://arxiv.org/abs/2402.03300
GRPO,即组相对策略优化(Group Relative Policy Optimization),是一种创新的强化学习算法,提升大语言模型在复杂任务(如数学推理、编程)中的表现,旨在通过比较同一组内不同策略或动作的相对表现来优化学习过程。而不是依赖传统的批评者模型(Critic Model)来评估每个动作的价值。
GRPO 的核心思想是让智能体通过与其他智能体或自身生成的多个候选动作进行对比,利用群体得分的相对差异来进行策略更新,从而降低计算成本并提高训练效率。
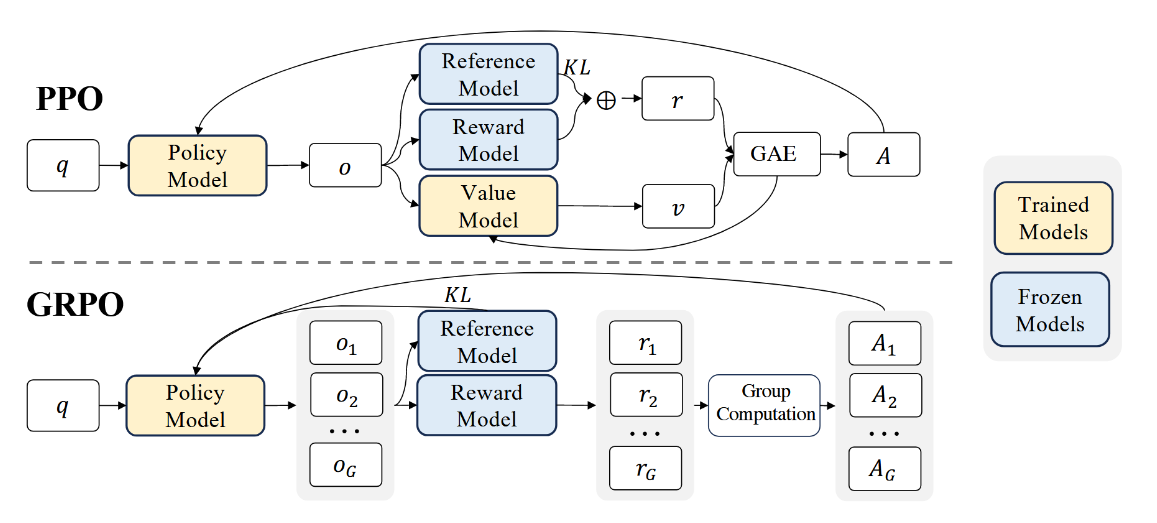
GRPO 是 Proximal Policy Optimization(PPO)的改进版本,主要优化点包括:
- 省略 Critic 模型:无需单独训练价值函数(Critic),直接通过组内样本的平均奖励作为基线。
- 组内相对优势计算:通过同一提示下生成的多个响应(组)之间的比较,估计每个样本的优势值。
- 资源效率:内存消耗减少约 25%(因无需 Critic 模型),适合资源受限场景
# PPO
PPO(Proximal Policy Optimization)是一种用于强化学习的策略优化算法,由 OpenAI 提出。它通过限制策略更新的幅度,确保训练过程的稳定性。
PPO 的核心在于限制策略更新的幅度,避免因更新过大导致性能下降。它通过引入 “裁剪” 机制,控制新旧策略之间的差异。
PPO 算法,参与训练的有 4 个模型。分别是 Policy model、Reference model、Reward model 和 Value model。
Policy model: 被训练的模型,根据问题 q 生成答案 o,可以更新梯度。
Reference model: 参考模型,一般与 Policy model 同源,但是参数是冻结的,不可更新梯度,输入问题 q,输出答案的概率分布,它用于约束 Policy model 的更新幅度,确保梯度更新后的 Policy model 输出的概率分布与 Reference model 相差不要太大。
Reward model: 奖励模型,负责给整个结果(问题 + 答案)打分。一般需要使用偏好数据集,单独训练一个 reward 模型。
Value model:价值模型,也叫 critic model,可以更新梯度,用于预测当前 token 到结束时的期望回报。
# 优势函数
Advantage 函数用于衡量在某个状态(State)下,采取某个动作(Action)相对于平均表现的优劣程度。它的数学定义为 $$A (s,a)=Q (s,a)-V (s)$$:, 其中:
A(s,a)$$是**优势函数**,表示在状态 下采取动作 比平均表现好多少(或差多少)。 如果$$A(s,a)>0$$ ,说明动作 a 比平均表现更好,策略应该更倾向于选择这个动作; ##### KL penalty KL Penalty是基于**KL散度(Kullback-Leibler Divergence)**的一种正则化手段。KL散度用于衡量两个概率分布之间的差异。在强化学习中,KL Penalty通常用于限制当前策略$$\pi_{\theta}$$ 和参考策略 $$\pi_{ref}$$ 之间的差异。其数学定义为:$$D_{KL} (\pi_{\theta} \| \pi_{ref}) \pi_{\theta}$$是当前策略(由模型参数 决定)。 $$\pi_{ref}$$是参考策略(通常是更新前的策略或某个基线策略)。 KL Penalty用于防止策略更新过大,确保当前策略不会偏离参考策略太远。这样可以避免训练过程中的不稳定现象。KL Penalty就像一个“约束”,告诉模型在更新策略时不要“步子迈得太大” ##### 分组机制 组生成:对每个输入问题生成多个候选答案(如5个),构成一个组(Group) 通过组内奖励的均值和标准差,计算每个样本的相对优势 $$\tilde{r_i}=\frac{r_i-\mu}{\sigma}$$, $$r_i$$是样本奖励,$$\mu 是均值 , \sigma 是标准差
# 目标函数
KL 散度正则项:防止策略偏离参考模型 (如 SFT 模型) 过远参数 β 控制正则强度
重要性采样比 (Policy Ratio):衡量新旧策略之间的变化。
裁剪的目标函数 (Clipped Objective):限制策略更新幅度,以避免剧烈变化导致模型崩溃。
KL 散度正则项 (KL Divergence Regularization):确保新策略不会偏离参考策略太远,以保持稳定性。
优势估计 (Advantage Estimate) Ai 衡量 oi 在同一组候选响应中的相对质量。这种 归一化优势估计 可以减少奖励尺度的影响,提高训练稳定性。

# 对目标函数举例
7 + 3*7 = ?假设 采样了 4 组不同的输出(G=4)
针对 "What is 7 + 3*7 = ?" 这个问题,模型可能生成以下 4 种答案:
o1:
7 + 3 = 10, 10 * 7 = 70 70 运算顺序错误
o2:
3 * 7 = 21, 21 + 7 = 28 28 答案正确
o3:
28 答案正确,但缺少
标签 o4:
… 一些混乱的推理… 7 答案错误,且推理过程混乱
然后使用基于规则的两个奖励:准确性奖励、格式奖励(实践中,奖励函数是可以按需设计的,可以规则奖励,也可以偏好奖励,无论哪种奖励,都可以用 GRPO),对上面的 4 个输出分别进行奖励评分,假设奖励的分配如下
| 输出 | 准确性奖励 | 格式奖励 | 总奖励 |
|---|---|---|---|
| o1 (答案错误) | 0 | 0.1 | 0.1 |
| o2 (答案正确) | 1 | 0.1 | 1.1 |
| o3 (答案正确,但缺少格式标签) | 1 | 0 | 1.0 |
| o4 (推理混乱且答案错误) | 0 | 0.1 | 0.1 |
有了每个输出所对应的奖励,便可以计算奖励值的均值、优势值
根据优势计算公式 $$A_i=\frac {r_i-\mu}{\sigma}$$ 计算优势值
回答优于小组平均水平的,将获得正分,而回答较差的,将获得负分。鼓励群体内部竞争,推动模型产生更好的反应。
输出 o2 和 o3 具有正优势,说明它们应该被鼓励;而 o1 和 o4 具有负优势,意味着它们应该被抑制。GRPO 使用这些计算得到的优势值来更新策略模型
调整模型(πθ)以偏好具有较高优势值(Ai>0)的响应,同时避免大幅度的不稳定更新:如果新策略与旧策略的比率超出范围 [1−ϵ,1+ϵ],则会被裁剪以防止过度修正。
添加一个惩罚项 $$\beta D_{KL} (\pi_{\theta} | \pi_{\text {ref}})$$ 以确保更新后的策略 $$\pi_{\theta}$$ 不会偏离参考策略 $$\pi_{\text {ref}}$$ 太远。
- 无需批评:GRPO 依靠群体比较避免了对单独评估者的需求,从而降低了计算成本。
- 稳定学习:剪辑和 KL 正则化确保模型稳步改进,不会出现剧烈波动。
- 高效训练:通过关注相对性能,GRPO 非常适合推理等绝对评分困难的任务。
# Deepseek-R1
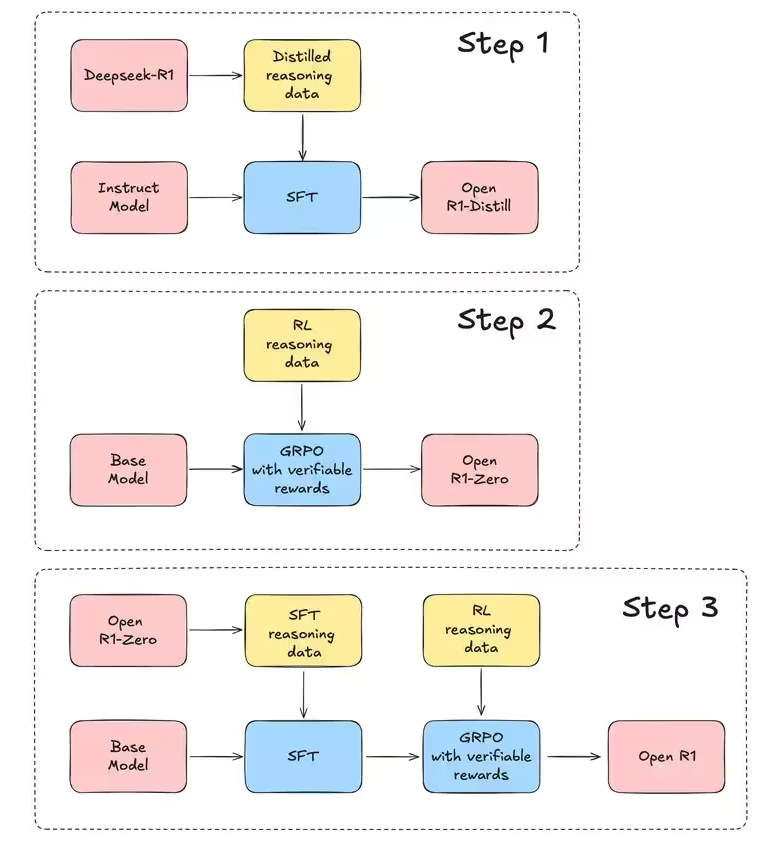
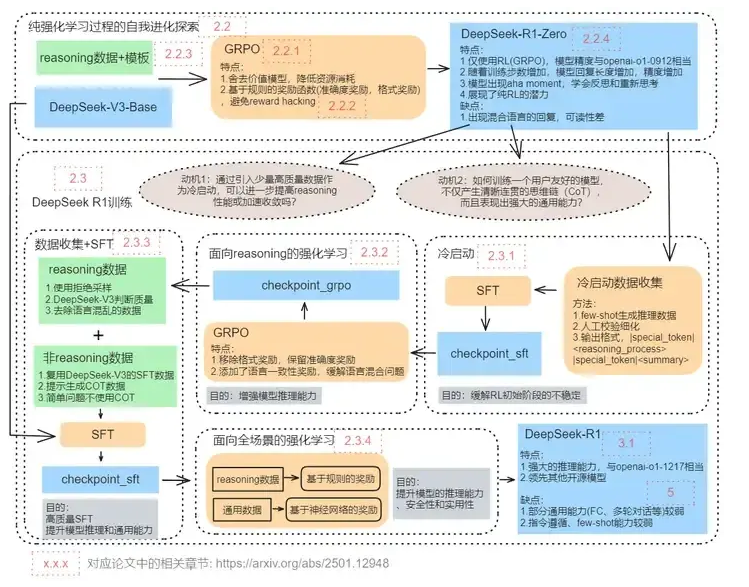
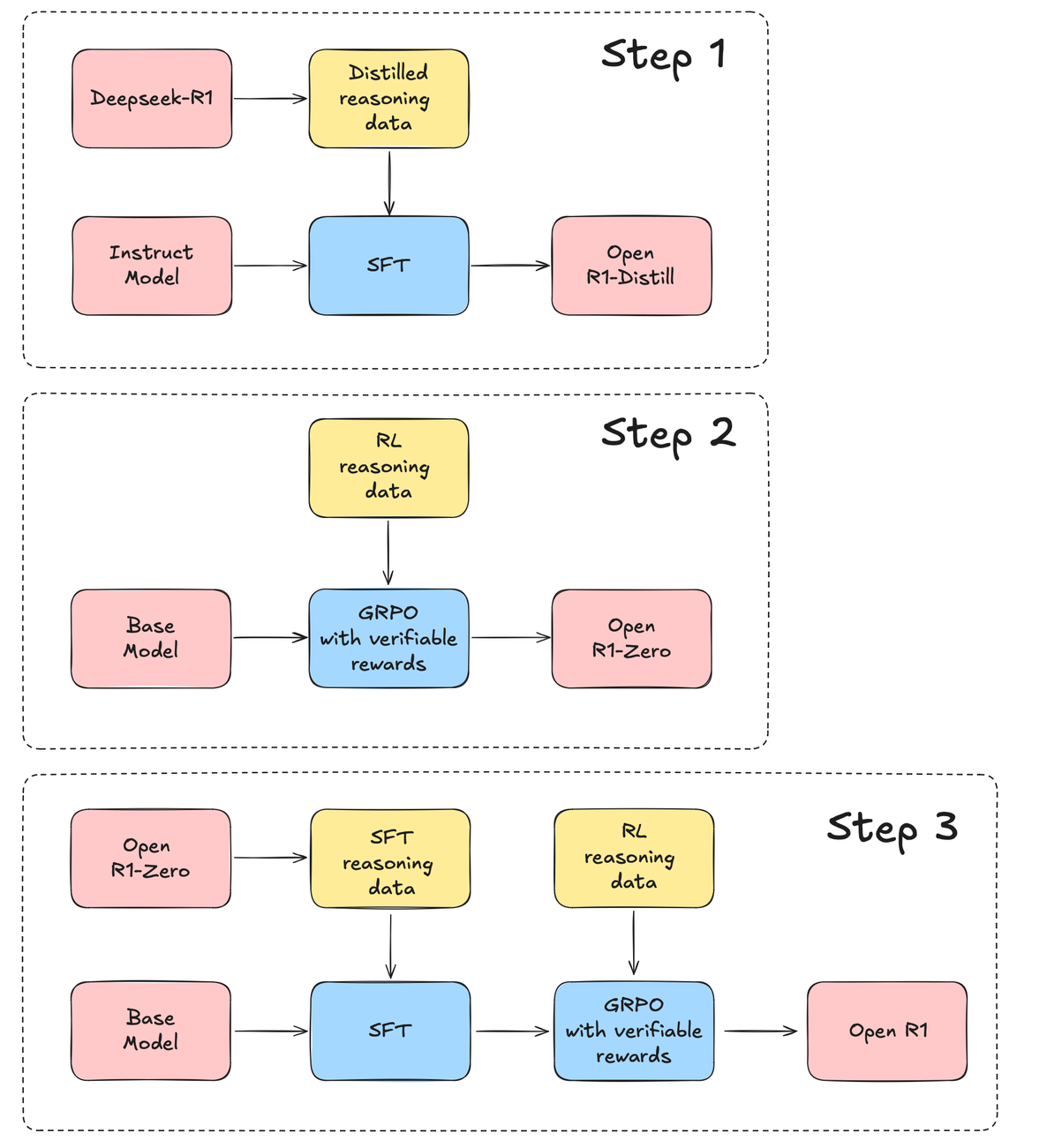
Step 1 是蒸馏 Distill 的过程。这一部分是在 Deepseek-R1 训练完成后,基于该模型生成一些训练数据,对 Qwen、Llama 等小型模型做简单的 SFT。输入是各类输出是各种版本的 distill 模型。
Step 2 是一个强化学习 RL 过程,使用了 GRPO。输入是 base model(论文中是 Deepseek-v3-Base)、推理数据中的问题,输出是 R1-zero 模型。
Step 3 是完整的 R1 训练过程,包括 SFT 和 GRPO 两个阶段,首先,对 base model 做 SFT,训练数据来自于 R1-zero,以及其他方式收集,然后对 SFT 后的模型,再做一个完整的 GRPO,等到最终的 R1 模型。
https://article.juejin.cn/post/7470102625934082098
https://www.bilibili.com/read/cv41808868
https://www.cnblogs.com/GreenOrange/p/18726311
https://mp.weixin.qq.com/s?__biz=MzI4MDYzNzg4Mw==&mid=2247569612&idx=3&sn=a3e0e3fd74c391da56fe39d2ac5ba62c&chksm=eab415c5169c91180f00186aa3bfd96a94950f17c03181a279828a0f097a44f874287699b45e&scene=27
https://blog.csdn.net/v_JULY_v/article/details/136656918
https://zhuanlan.zhihu.com/p/30331039302
# RLHF
训练阶段,如果直接用人的偏好(或者说人的反馈)来对模型整体的输出结果计算 reward 或 loss,显然是要比传统的 “给定上下文,预测下一个词” 的损失函数合理的多。基于这个思想,便引出了 RLHF(Reinforcement Learning from Human Feedback):即使用强化学习的方法,利用人类反馈信号直接优化语言模型。
基于人类反馈的强化学习(Reinforcement Learning from Human Feedback, RLHF)是一种结合强化学习(RL)与人类反馈(HF)的机器学习技术。它通过利用人类的直接反馈来训练 "奖励模型",然后使用该模型通过强化学习优化 AI 代理(尤其是大型语言模型)的性能。RLHF 也被称为 "基于人类偏好的强化学习",特别适用于处理目标复杂、定义不明确或难以精准表述的任务。
RLHF 的理论基础建立在强化学习和人类偏好学习两个领域的交叉点上:
- 强化学习:通过试错学习最大化累积奖励的计算方法
- 人类偏好学习:从人类评估中提取价值信息的技术
这种结合使 RLHF 能够在没有明确定义奖励函数的情况下,通过人类反馈来指导 AI 系统的行为。
# RLHF 流程
RLHF 训练流程通常包含四个关键阶段,每个阶段都有其特定的目的和方法:
# 预训练阶段
预训练是 RLHF 流程的基础,但严格来说并不属于 RLHF 本身。在这个阶段:
- 使用大规模文本数据训练初始语言模型
- 模型学习语言的基本结构、语法和知识
- 采用自监督学习方法(如下一个词预测任务)
- 这是整个流程中最耗费计算资源的阶段
预训练模型为后续的 RLHF 过程提供了基础能力,但通常缺乏对特定任务的理解和对齐人类偏好的能力。
# 监督微调(SFT)
在正式进入强化学习阶段之前,需要利用监督微调 (SFT) 来引导模型,使其生成的响应符合用户的预期格式。有时,LLM 不会按照用户想要的方式完成序列:例如,如果用户的提示是 “教我如何制作简历”, LLM 可能会回答 “使用 Microsoft Word。” 这是完成句子的有效方法,但与用户的目标不符。
SFT 使用监督学习来训练模型,以便对不同类型的提示做出适当的响应。人类专家按照格式 (提示,响应) 创建带标签的示例,演示对于不同的用例,例如回答问题、摘要或翻译,如何回应提示。
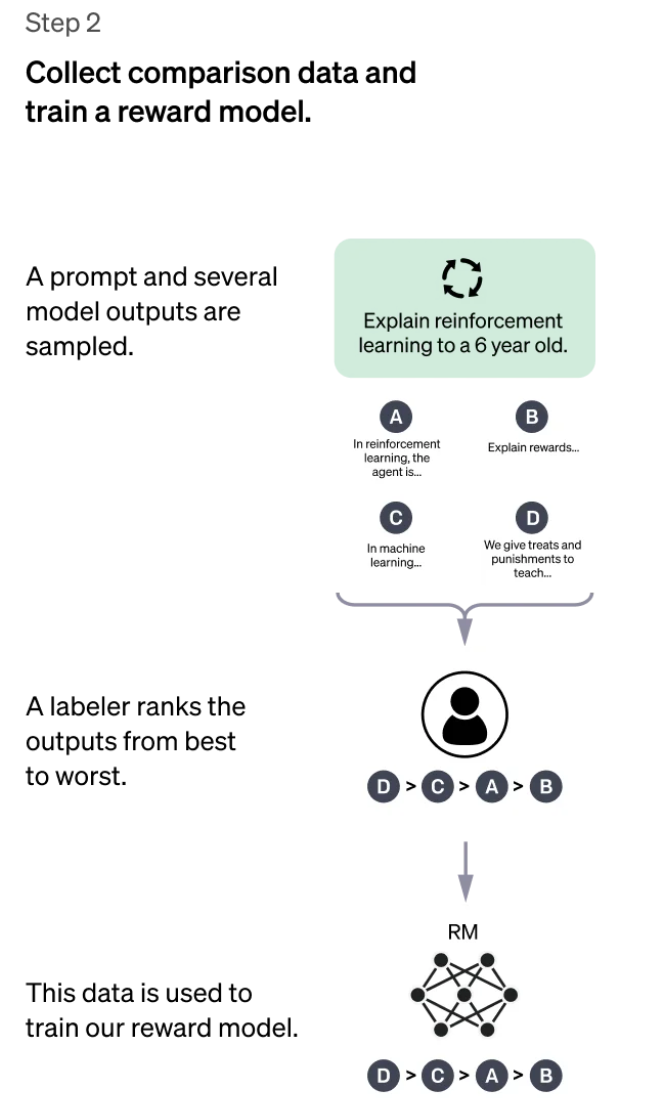
# 奖励模型训练(RM)
为了在强化学习中为奖励函数提供人类反馈,需要一个奖励模型来将人类偏好转化为数字奖励信号。设计有效的奖励模型是 RLHF 的关键一步
此阶段的主要目的是为奖励模型提供足够的训练数据,包括来自人类评估者的直接反馈,以帮助模型学习模仿人类依据其偏好将奖励分配给不同种类的模型响应的方式。
目的
- 构建一个能够评估文本质量并与人类判断一致的模型
- 为强化学习阶段提供奖励信号
- 解决传统强化学习中奖励函数难以定义的问题
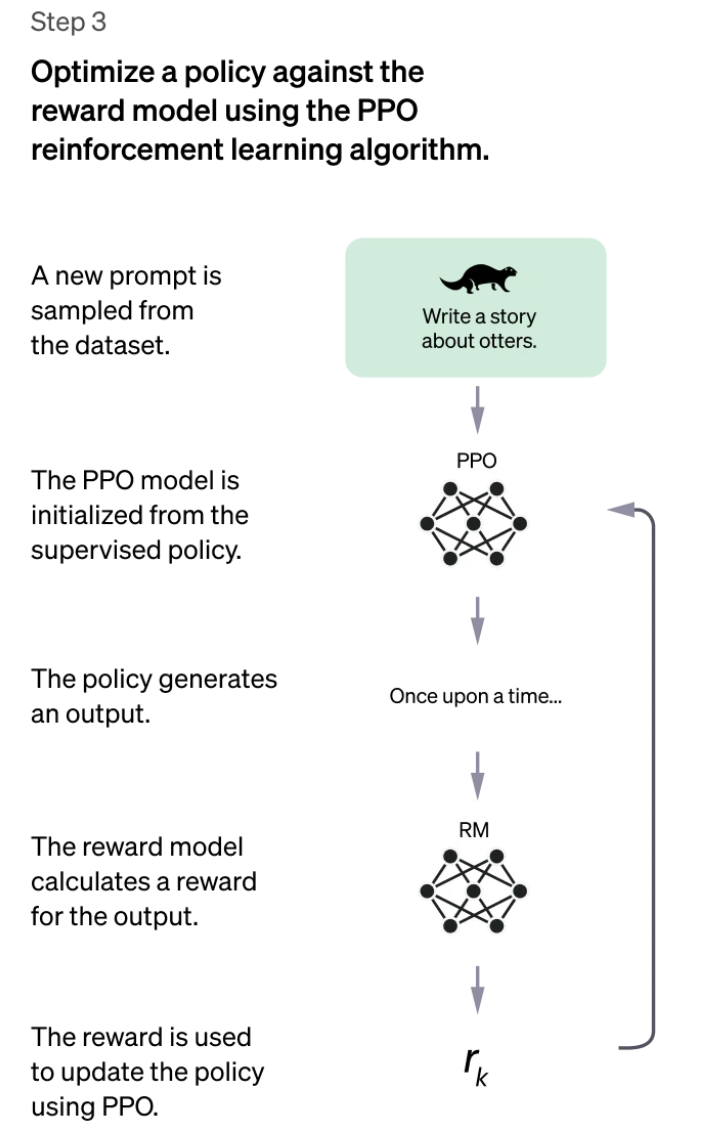
# 策略优化
策略优化是 RLHF 的最后一个阶段,也是真正的 "强化学习" 部分。用于更新 RL 模型的奖励函数的最成功算法之一是近端策略优化 (PPO)。
如果在没有任何惩罚的情况下使用奖励函数来训练 LLM,则语言模型可能会为了迎合奖励机制而大幅调整其权重,甚至输出毫无意义的胡言乱语。PPO 会限制每次训练迭代中可以在多大程度上更新策略,从而提供了一种更稳定的更新 AI 代理策略的方法。
目的
- 使语言模型生成的文本能够最大化奖励模型的评分
- 同时保持文本的连贯性和多样性
- 避免过度优化导致的问题(如生成无意义但能获得高奖励的文本)

# 原理
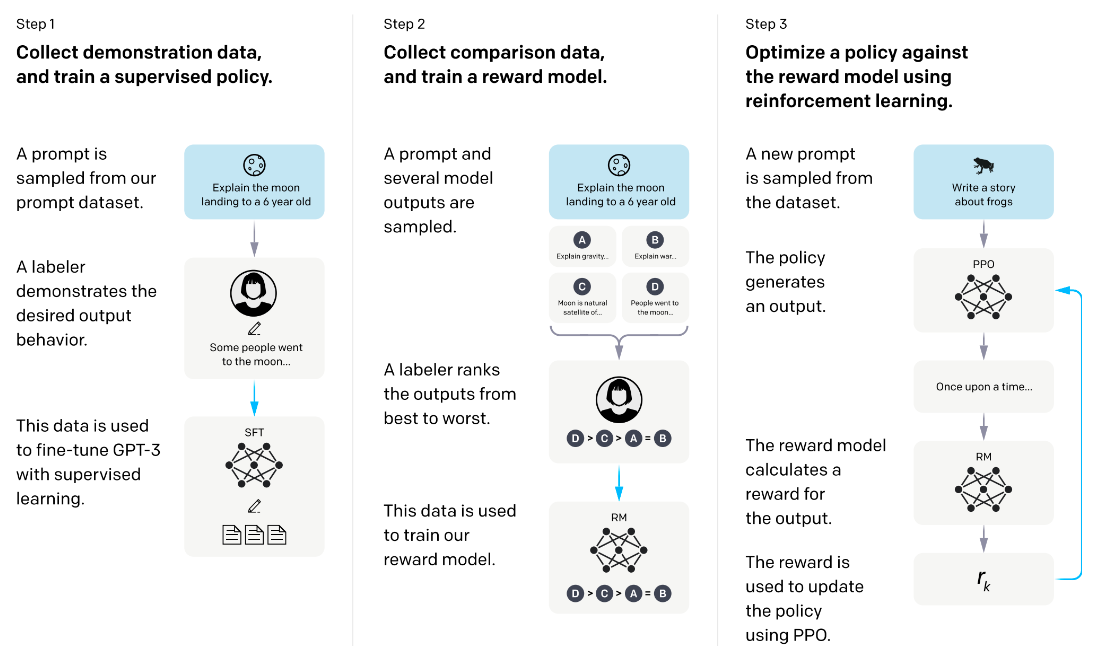
# Step 1:预训练语言模型 + 有标签数据微调(可选)
首先需要一个预训练语言模型,通过大量的语料去训练出基础模型,对于 ChatGPT 来说就是 GPT-3。还有一个可选的 Human Augmented Text, 又叫 Fine-tune。这里就是招人给问题(prompt)写示范回答(demonstration),然后给 GPT-3 上学习。Fine-tune 又叫有标签数据微调,概念比较简单,就是给到标准答案让模型去学习,
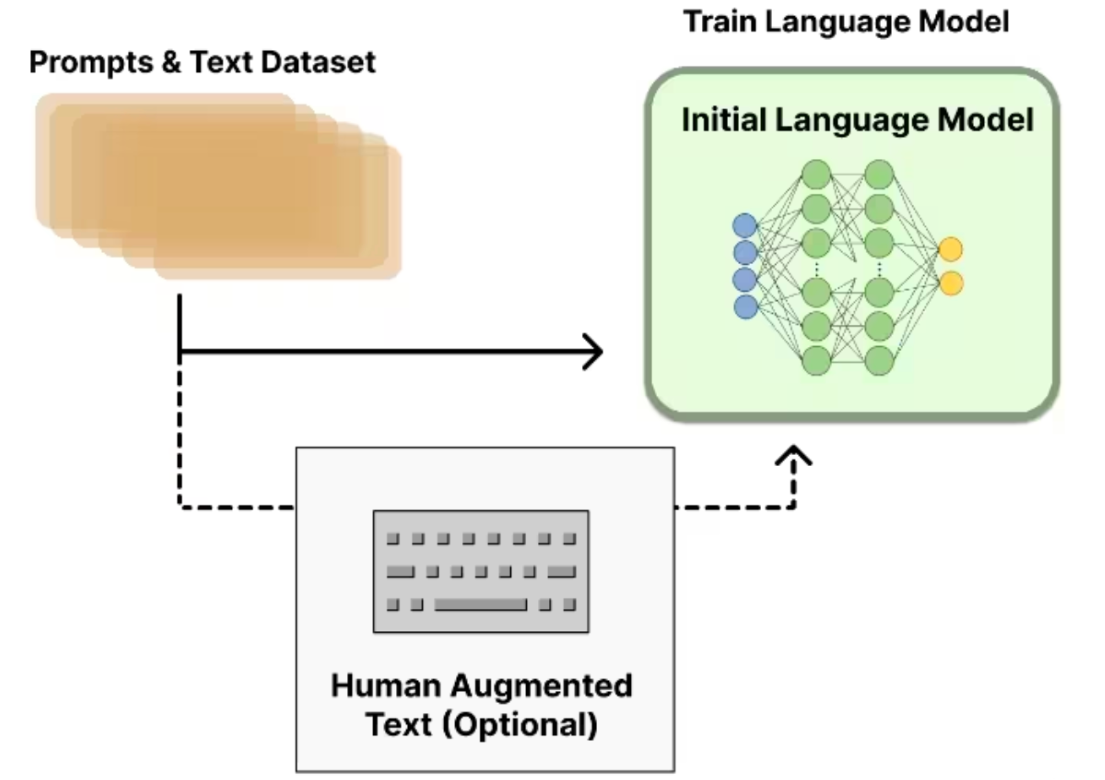
# Step 2:训练奖励模型
我们需要一个模型来定量评判模型输出的回答在人类看来是否质量不错,即输入 [提示 (prompt),模型生成的回答] ,奖励模型输出一个能表示回答质量的标量数字。
- 把大量的 prompt(Open AI 使用调用 GPT-3 用户的真实数据)输入给第一步得到的语言模型,对同一个问题,可以让一个模型生成多个回答,也可以让不同的微调(fine-tune)版本回答。
- 让标注人员对同一个问题的不同回答排序,有人可能会好奇为啥不打分?这是因为实验发现发现不同的标注员,打分的偏好会有很大的差异,而这种差异就会导致出现大量的噪声样本。排序的话能获得大大提升一致性。
- 这些不同的排序结果会通过某种归一化的方式变成定量的数据丢给模型训练,从而获得一个奖励模型。也就是一个裁判员。
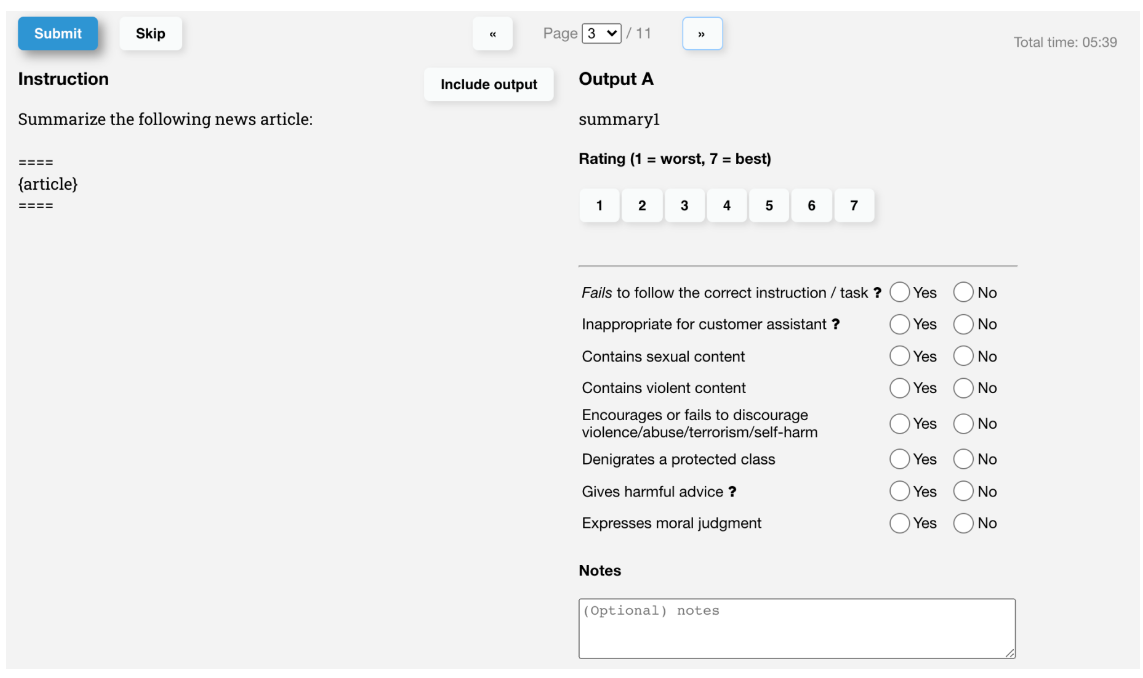

# Step 3:通过强化学习微调语言模型
基于强化学习(RL)去优化调整语言模型
- policy 是给 GPT 输入文本后输出结果的过程(输出文本的概率分布)
- Action Space 是词表所有 token(可以简单理解为词语)在所有输出位置的排列组合
- Observation space 是可能输入的 token 序列,也就是 Prompt
- Reward Function 则是基于上面第二步得到的奖励模型,配合一些策略层面的约束
- 将初始语言模型的微调任务建模为强化学习问题,因此需要定义策略(policy)、动作空间(action space)和奖励函数(reward function)等基本要素
- 具体怎么计算得到奖励 Chat GPT 是基于梯度下降,Open AI 用的是 Proximal Policy Optimization (PPO) 算法。
# RLHF 缺陷
1. 人类反馈的高成本
2. 人类偏好的主观性
3. 多样性减少问题
- RLHF 可能导致模型输出过于集中
- 创造性和多样性可能被牺牲
- 模型可能过度优化以迎合特定类型的反馈
4. 奖励黑客问题
- 模型可能学会 "欺骗" 奖励函数
- 生成表面上看起来好但实际无用的输出
- 需要更复杂的奖励设计和约束
# 自回归和非自回归
自回归(Auto-Regressive)
自回归生成是指序列生成过程中,每个新生成的 token 依赖于之前生成的 token。这意味着生成过程是串行的,每一步的输入由前面已生成的 token 组成的上下文序列构成。
假设要生成一个长度为 T 的句子 y=(y1,y2,…,yT),在生成句子 y 的过程中,首先生成 y1,然后在生成 y2 时需要考虑 y1;在生成 y3 时,需要考虑 (y1,y2),以此类推,直到生成结束符号( <end> )。
非自回归(Non-Autoregressive)
非自回归生成是一种并行生成的方式,一次性生成多个甚至全部的 token,从而显著提高生成速度,但也会牺牲一定的生成质量。
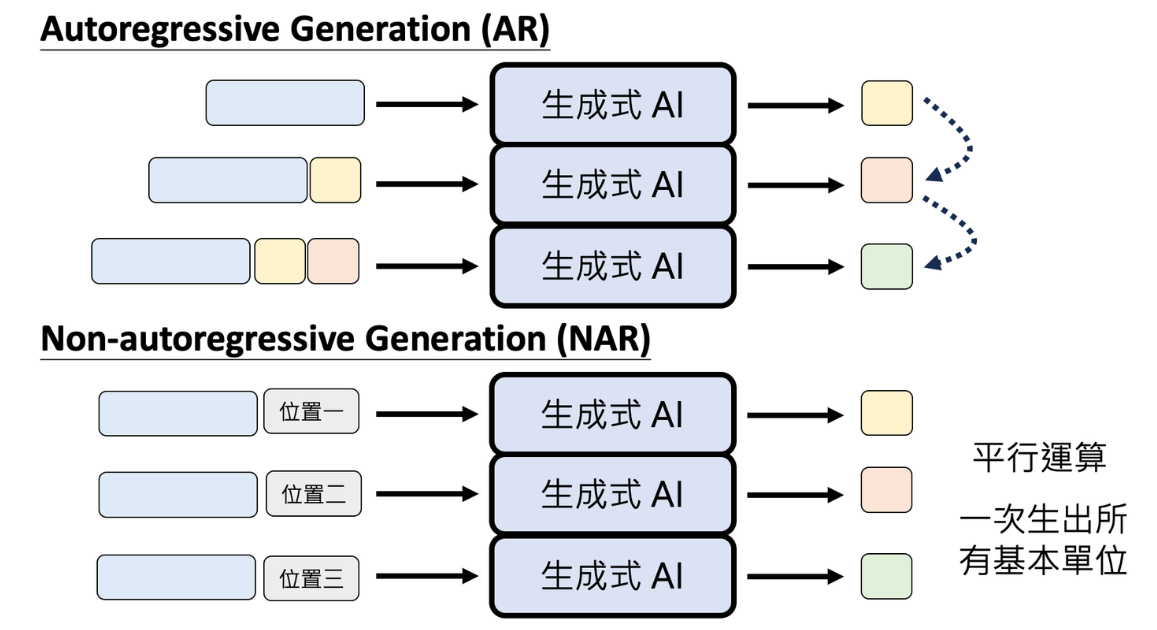
# InstructGPT 中 RLHF 的应用
论文原文:https://arxiv.org/pdf/2203.02155
# 1、使用 RLHF 背景
大型语言模型(例如 GPT-3)基于来自互联网的海量文本数据进行训练 ,能够生成类似人类的文本 ,但它们的输出可能并不总是符合人类的预期或理想值。事实上,它们的目标函数是单词序列(或标记序列)的概率分布,这使得它们能够预测序列中下一个单词是什么。
虽然这些基于海量数据训练的强大而复杂的模型在过去几年中已经变得非常强大,但在用于简化人类生活的生产系统中时,它们往往无法充分发挥其潜力。大型语言模型中的对齐 (alignment) 问题通常表现为:
- 缺乏帮助:不遵循用户的明确指示。
- 幻觉:模型编造不存在或错误的事实。
- 缺乏可解释性:人类很难理解模型如何得出特定的决策或预测。
- 生成有偏见或有害的输出:使用有偏见 / 有害数据训练的语言模型可能会在其输出中重现这种输出,即使没有明确指示这样做。
Next-token-prediction 和 masked-language-modeling 是训练语言模型(例如 Transformer )的核心技术 。在第一种方法中,模型被赋予一个单词序列(或 “词元”,即单词的一部分)作为输入,并被要求预测该序列中的下一个单词。
这些训练策略可能会导致语言模型在某些更复杂的任务上出现偏差,因为一个只被训练来预测文本序列中下一个单词(或被屏蔽的单词)的模型,可能不一定会学习到其含义的更高级表示。
通过使用人工反馈来指导学习过程进行了进一步训练,其具体目标是缓解模型的对齐问题。所使用的具体技术称为 “基于人工反馈的强化学习”,
# 2、InstructGPT 对于 RLHF 的实现
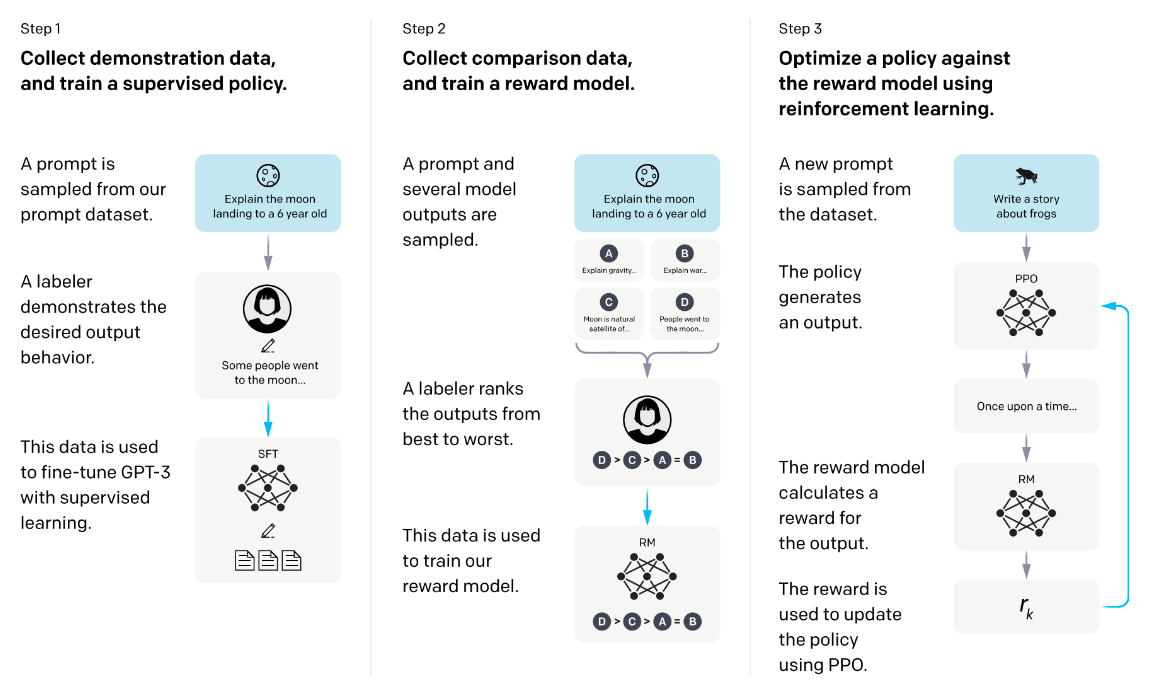
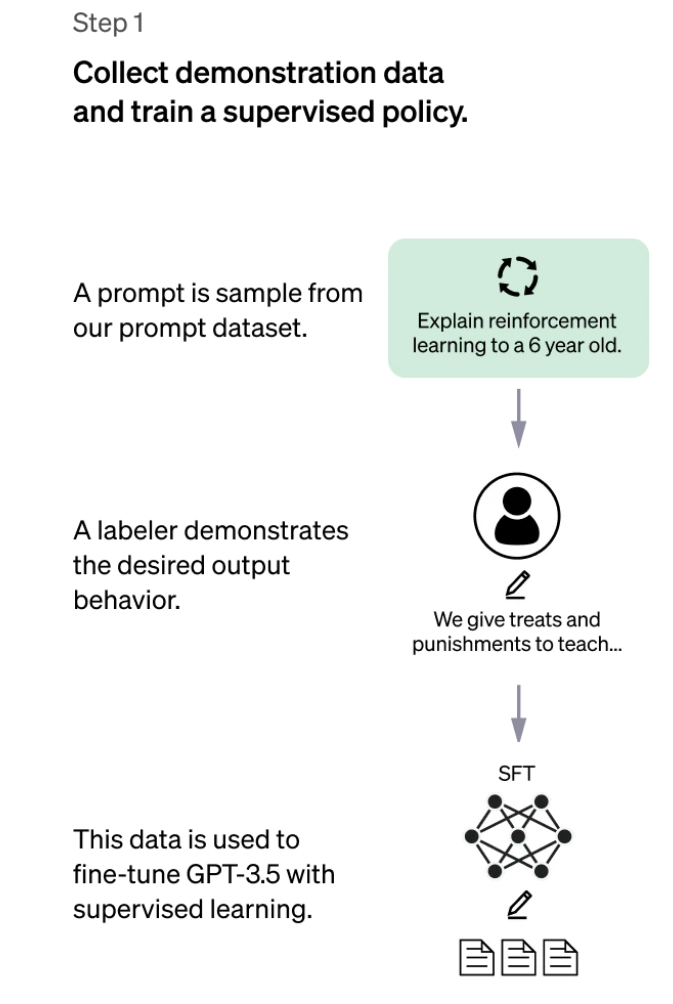
使用 RLHF 对 ChatGPT 进行微调包括三个不同的步骤:
1、监督微调 —— 基于标注员整理的相对少量的演示数据,对预训练的语言模型进行微调,以学习监督策略 ( SFT 模型 ),该策略可根据选定的提示列表生成输出。这代表了基线模型。
数据收集:选择一系列 Prompt,并要求一组人工标注员写下预期的输出响应 。对于 ChatGPT,使用了两种不同的提示来源:一些提示直接来自标注员或开发人员准备,一些提示则来自 OpenAI 的 API 请求(例如来自其 GPT-3 客户)。由于整个过程缓慢且成本高昂,最终结果是一个相对较小但高质量的精选数据集(大概包含 12,000-15,000 个数据点),用于微调预训练语言模型。
由于此步骤的数据量有限,经过此过程获得的 SFT 模型很可能输出的文本仍然(概率上)不太吸引用户注意,并且通常存在 alignment 问题,监督学习步骤的可扩展性成本很高。
为了解决这个问题,现在的策略不是要求人工标注员创建更大的精选数据集(这是一个缓慢而昂贵的过程),而是让标注员对 SFT 模型的不同输出进行排序以创建奖励模型
2、“模仿人类偏好” —— 标注员被要求对 SFT 模型输出的相对大量的数据进行投票,从而创建一个由比较数据组成的新数据集。并在此数据集上训练一个新模型。这被称为奖励模型(RM) 。
目标是直接从数据中学习一个目标函数(奖励模型)。该函数的目的是为 SFT 模型的输出赋予一个分数,该分数与这些输出对人类的吸引力成正比。这将强烈反映所选人类标注者群体的特定偏好以及他们同意遵循的共同准则。最终,这个过程将从数据中提取出一个旨在模仿人类偏好的自动化系统。
1、选择提示列表,SFT 模型为每个提示生成多个输出(介于 4 到 9 之间)。
2、标注器将输出结果按从好到坏的顺序排列。结果会生成一个新的带标签数据集,其中的排名即为标签。该数据集的大小大约是 SFT 模型所用精选数据集的 10 倍。
3、这些新数据用于训练奖励模型 (RM)。该模型将 SFT 模型的部分输出作为输入,并按优先顺序进行排序。
对于标注员来说,对输出进行排序比从头开始生成输出要容易得多, 这个过程的扩展效率也更高 。实际上,该数据集是从 3 万到 4 万个问题中生成的,并且在排序阶段,每个问题生成的输出(数量不定)会呈现给每个标注员。
3、近端策略优化 (PPO) – 使用奖励模型进一步微调和改进 SFT 模型。此步骤的结果就是所谓的策略模型 。
强化学习被应用于微调 SFT 策略,使其优化奖励模型。所使用的具体算法称为近端策略优化 (PPO),经过微调的模型称为 PPO 模型。
在此步骤中,PPO 模型由 SFT 模型初始化, 价值函数由奖励模型初始化 。环境是一个多臂老虎机 ,它会给出一个随机 prompt,并期望玩家对该提示做出 completion。在给出提示和响应后,游戏会产生一个奖励(由奖励模型决定),然后游戏结束。SFT 模型会在每个 token 上添加一个基于 token 的 KL 惩罚 ,以缓解奖励模型的过度优化。
步骤 1 只发生一次,而步骤 2 和 3 可以不断迭代:在当前最佳策略模型上收集更多的比较数据,用于训练新的奖励模型,然后训练新的策略。
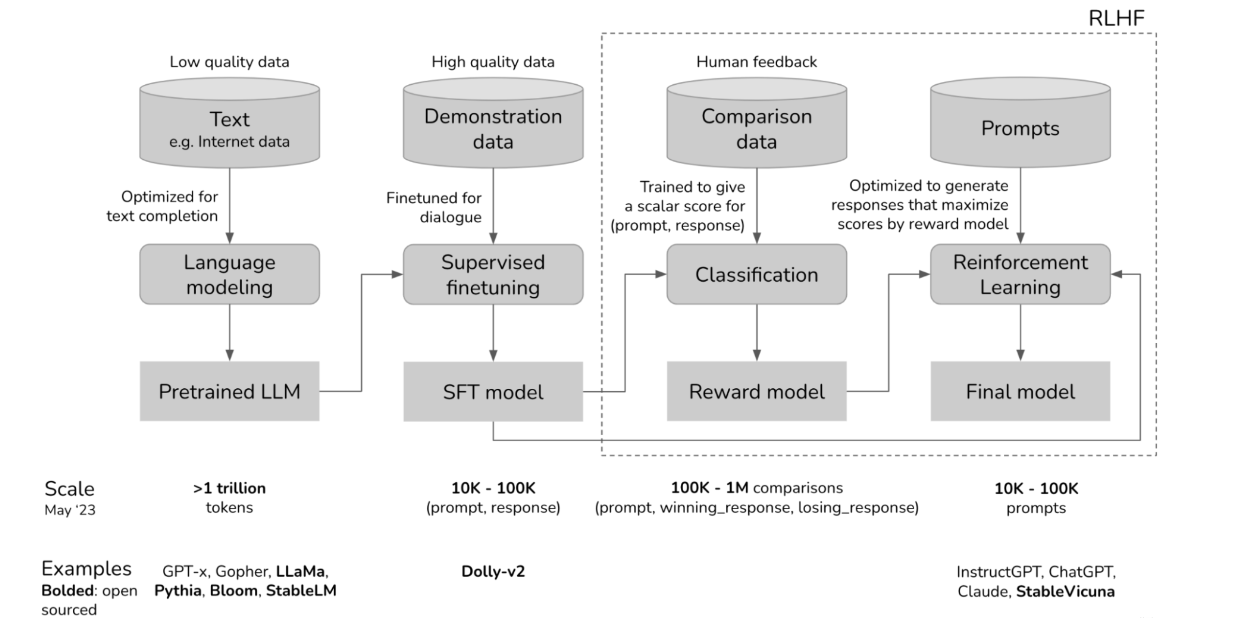
RLHF 激发了基础模型的能力。重要的数据质检,减少噪声
# 3、评估
由于该模型是基于人工标注员的输入进行训练的, 因此评估的核心部分也基于人工输入 ,即通过让标注员对模型输出的质量进行评分来进行。为了避免过度拟合训练阶段标注员的判断,测试集使用了来自 OpenAI 客户的 Prompt,这些提示未在训练数据中出现。
1、有用性:判断模型遵循用户指令以及推断指令的能力。
2、真实性:判断模型在 close-domain 任务中产生幻觉(即编造事实)的倾向。该模型在 TruthfulQA 数据集上进行评估。
3、无害性:标注者评估模型的输出是否恰当、是否贬低受保护的群体或是否包含贬损性内容。该模型还在 RealToxicityPrompts 和 CrowS-Pairs 数据集上进行了基准测试。
InstructGPT 模型在真实性方面比 GPT-3 有所改进。在 TruthfulQA 基准测试上,我们的 PPO 模型生成真实且信息丰富的答案的频率大约是 GPT-3 的两倍。
InstructGPT 在毒性方面比 GPT-3 略有改进,但在偏见方面没有显著改善。
该模型还在问答、阅读理解和摘要等传统 NLP 任务上进行了零样本性能评估, 开发人员观察到其中一些任务的性能与 GPT-3 相比有所下降 。这是一个 “alignment tax” 的例子,基于 RLHF 的对齐程序是以某些任务的性能下降为代价的。
# 4、缺陷
用于微调模型的数据会受到各种复杂的主观因素的影响,包括:
- 制作演示数据的标记者的偏好。
- 设计研究并撰写标签说明的研究人员
- 打标签人员的偏见既包含在奖励模型训练中(通过对输出进行排序)
- 在强化学习方法中,模型有时会学习操纵自身的奖励系统以达到预期结果,从而导致 “策略过度优化”。
- 奖励模型 (RM) 的提示稳定性测试 :目前似乎没有实验研究奖励模型对输入提示变化的敏感性。
- 缺乏对比数据的真实性 :标注员对模型输出的排序常常意见不一。
# 5、论文补充
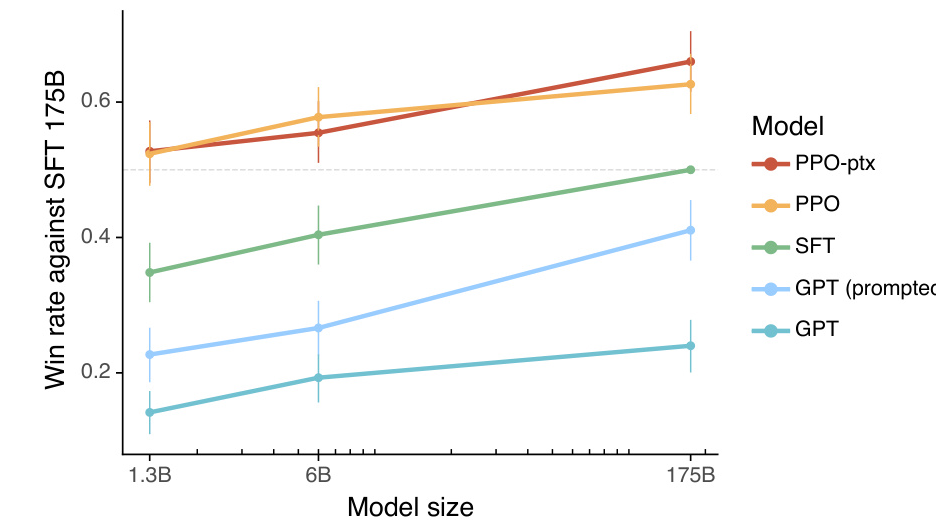
PPO-ptx InstructGPT,在 PPO 期间加入预训练混合
SFT 数据集包含约 13,000 条训练提示(来自 API 和标注员编写),RM 数据集包含 33,000 条训练提示(来自 API 和标注员编写),PPO 数据集包含 31,000 条训练提示(仅来自 API)
本文中,我们仅使用了 6B RM,因为这可以节省大量计算资源。我们发现,175B RM 的训练可能不稳定,因此不太适合用作强化学习中的值函数
为了加快比较结果的收集,我们向标注者提供数量在 K = 4 到 K = 9 之间的回复,让他们进行排序。
Reward Model Loss function
其中 $$r_{\theta}(x,y)$$ 是带有参数 $$\theta$$ 的 prompt $$x$$ 与 completion $$y$$ 的奖励模型的标量输出,$$y_{w}$$ 是 $$y_{w}$$ 和 $$y_{l}$$ 这一对 completion 中的更好的内容,$$D$$ 是人工比较数据集。
我们使用偏差对奖励模型进行归一化处理,以便在进行强化学习(RL)之前,标注者的示范样本平均得分达到 0。
objective function
我们还尝试将预训练梯度与近端策略优化(PPO)梯度混合,以解决公共自然语言处理(NLP)数据集上的性能退化问题。
其中, $$\pi_\phi}}$$ 表示学习到的强化学习策略, $$\pi^{\mathrm {SFT}}$$ 表示监督训练模型, $$D_{\textrm {pretrain}}$$ 表示预训练分布。KL 奖励系数 $$\beta$$ 和预训练损失系数 $$\gamma$$ 分别控制 KL 惩罚和预训练梯度的强度。对于 “PPO” 模型, $$\gamma$$ 设置为 0。
尝试将自然语言生成任务往 Actor-Critic 的框架里套。RLHF 的基本算法思路仍符合 Actor-Critic 框架。
我们共有 4 个模型:
- 当前正在训练的演员(ChatGPT)
- 当前正在训练的评论家(ChatGPT + 的最后一层后面接一个新网络,ChatGPT 的参数与演员是共享的)
- 原始模型(GPT-3)
- reward model
其中前两个模型的参数是会在训练中改变的,后两个模型的参数是固定的。整体的步骤是:
- 演员行动:演员用当前 token 序列生成新 token,也就是 a_t
- 评论家估计:评论家估计动作价值 Q (s_t, a_t)
- 演员更新参数:用梯度 $$\nabla \log p (a_t|s_t) Q (s_t, a_t) $$ 来更新演员模型的参数
- 环境反馈:环境收到 a_t 之后给出新的 token 序列 $$s_{t+1} = Actor_Model (s_t ; a_t)$$ 然后调用 reward model 计算 $$r_{t+1}$$(过程中要用到旧模型 GPT-3),更新参数后的演员用新序列 $$s_{t+1}$$ 再生成下一个 token,也就是 $$a_{t+1}$$
- 评论家更新参数:更新参数以缩小价值误差 $$Q (s_{t+1}, a_{t+1}) + r_{t+1} - Q (s_t, a_t)$$
https://www.assemblyai.com/blog/how-chatgpt-actually-works?continueFlag=1bafdcd5c034def869fecb4f3bdaed70
https://www.assemblyai.com/blog/how-rlhf-preference-model-tuning-works-and-how-things-may-go-wrong
https://download.csdn.net/blog/column/12545383/135669376
https://openai.com/index/chatgpt/
https://www.ibm.com/cn-zh/think/topics/rlhf
https://bytetech.info/articles/7274183213785251901?from=baike_card#AcdQdlgKToz17FxCmsWc6poInlh
sparrow - deepmind
# DPO
Paper:https://arxiv.org/html/2305.18290v3
直接偏好优化 (DPO),这是一种简单的非强化学习 (RL-free) 算法,用于根据偏好训练语言模型。
DPO 算法直接利用人类偏好数据进行策略优化。想象你在学习画画,PPO 算法就像是你根据自己每次画画后的自我评价(环境奖励)来改进绘画技巧;而 DPO 算法则是直接参考老师或者其他专业人士对你画作的评价(人类偏好)来调整绘画方式。它通过构建一个偏好模型,将人类对不同策略产生的轨迹的偏好信息融入到策略更新中,从而使策略更符合人类的期望。
将偏好学习问题转化为策略模型的概率优化问题,直接通过偏好数据调整策略,无需独立奖励模型。
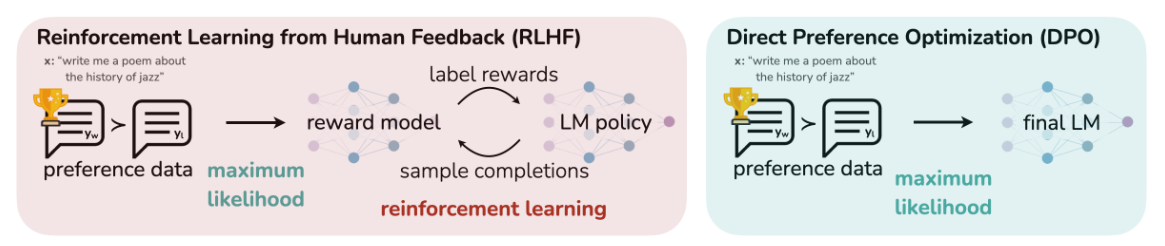
DPO 针对人类偏好进行优化,同时避免强化学习。 现有的利用人类反馈微调语言模型的方法,首先会将奖励模型拟合到包含提示和人类偏好的数据集上,然后使用强化学习找到最大化学习到的奖励的策略。相比之下,DPO 则直接利用简单的分类目标来优化最符合偏好的策略,即拟合一个隐式奖励模型,该模型对应的最优策略可以以闭包形式提取出来。
# 准备工作
SFT
RLHF 通常首先使用监督学习对高质量数据进行微调,以完成感兴趣的下游任务(对话、总结等),从而获得模型 $$π_{SFT}$$ 。
Bradley-Terry 偏好概率模型
假设人类偏好遵循 Bradley-Terry 模型,即对于偏好对 $$(y_w \succ y_l | x)$$,其概率为:
传统 RLHF 需训练独立的奖励模型 $$R (x, y)$$ 来拟合此概率。
奖励建模阶段
SFT 模型根据提示 x 生成答案对 $$(y_1,y_2)\sim\pi^{\text {SFT}}(y\mid x)$$ 。然后,这些答案被呈现给人工标注者,标注者对其中一个答案表达偏好,记为 $$y_{w}\succ y_{l}\mid x$$ ;其中 $$y_{w}$$ 和 $$ y_{l}$$ 分别表示 $$(y_1,y_2)$$ 中标注者偏好和较不偏好的 completion 结果。
BT 模型规定,人类偏好分布 p∗ 可以写成:$$p^*(y_1 \succ y_2|x)=\frac\exp(r\exp(r $$
将问题定义为二分类问题,我们得到负对数似然损失:$$ \mathcal {L}R(r\phi, \mathcal{D}) = -\mathbb{E}{(x, y_w, y_l) \sim \mathcal{D}} \left[ \log \sigma \left( r\phi(x, y_w) - r_\phi(x, y_l) \right) \right]$$
其中,$$\sigma$$ 为逻辑函数。在语言模型 (LM) 中,网络 $$r_\phi}(x,y)$$ 通常使用 SFT 模型 $$\pi}(y\mid x)$$ 初始化,并在最终的 Transformer 层之上添加一个线性层。该线性层对奖励值进行单标量预测 。为了确保奖励函数具有较低的方差,先前的研究对奖励进行了归一化,使得对所有 x 都满足 $$\mathbb {E}{x,y\sim\mathcal{D}}\left[r(x,y)\right]=0$$ 。
强化学习微调阶段
在强化学习阶段,学习到的奖励函数用于向语言模型提供反馈。
其中 β 是控制与基础参考策略 πref (即初始 SFT 模型 πSFT )偏差的参数。实践中,语言模型策略 πθ 也被初始化为 πSFT 。增加的约束很重要,因为它可以防止模型偏离奖励模型准确的分布太远,同时保持生成多样性并防止模式崩溃为单个高奖励答案。
# objective function
其中,$$r_{pref}(s,a) $$ 是偏好奖励,$$\alpha$$ 是平衡系数, $$\pi_{ref}$$ 是参考策略。这个公式的意思是,在优化策略时,既要考虑人类偏好奖励(你画画得到的专业评价分数),又要控制新策略与参考策略(比如一些经典的绘画风格)之间的差异不要太大(通过 KL 散度来衡量)。
# RLHF 目标函数
在强化学习人类反馈(RLHF)中,目标是优化策略模型 $$\pi_{\theta}$$ 以最大化人类偏好奖励,同时避免偏离参考模型 $$\pi_{\text {ref}}$$ 太远。其目标函数为:
R(x,y) 是RM $$,$$\beta $$是惩罚系数 ###### 核心思想 奖励函数的重新参数化:DPO 的关键创新在于将奖励函数 R(x, y) 隐式地表示为策略模型 $$\pi_{\theta}$$ 和参考模型 $$\pi_{\text{ref}}$$ 的对数概率比: $$R(x, y) = \beta \log \frac{\pi_\theta(y | x)}{\pi_{\text{ref}}(y | x)}
推导动机: 通过将奖励函数与策略模型绑定,绕过了显式训练奖励模型的步骤,直接优化策略模型 $$π_θ$$ 。
Loss Function
计算损失函数对策略参数 $$\theta$$ 的梯度:
其中
- 当 $$\hat {r}_w > \hat {r}_l$$(策略对优质响应打分更高),梯度权重 $$\sigma (\hat {r}_l - \hat {r}_w)$$ 趋近于 0,抑制参数更新。
- 当 $$\hat {r}_w < \hat {r}_l$$(策略未能区分优劣),梯度权重趋近于 1,强化模型对 $$y_w$$ 的偏好。
- 隐式奖励建模:通过 πθ/πref 的概率比替代显式奖励函数。
- 损失函数设计:将偏好学习转化为二元分类问题的对数损失。
- 优化一致性:在理想条件下,DPO 与 RLHF 共享相同的最优策略,但避免了复杂的强化学习训练。
https://blog.csdn.net/qq_22866291/article/details/145560717
https://zhuanlan.zhihu.com/p/21105217213
# Minimax-M1
Paper 地址:https://www.arxiv.org/pdf/2506.13585
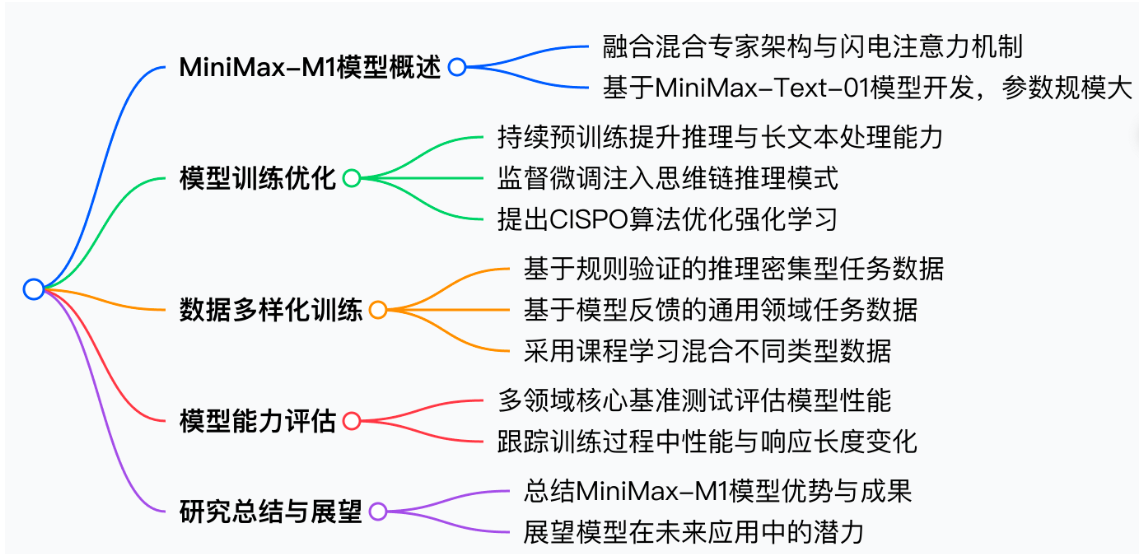
# Introduction
MiniMax-M1 采用混合专家(MoE)架构,并结合了 lightning attention。该模型基于我们之前的 MiniMax-Text-01 模型开发,包含总共 4560 亿个参数,每个标记激活 45.9 亿个参数和 32 个专家。M1 模型原生支持 100 万个 tokens 的上下文长度,是 DeepSeek R1 上下文大小的 8 倍。
MiniMax-M1 中的 lightning attention 使得测试时计算能够高效扩展 —— 例如,与 DeepSeek R1 相比,M1 在生成长度为 10 万个 tokens 时的 FLOPs 消耗仅为 25%。这些特性使 M1 特别适合需要处理长输入和进行广泛思考的复杂任务。
MiniMax-M1 使用大规模强化学习(RL)进行训练,训练数据涵盖了从传统数学推理到基于沙盒的真实世界软件工程环境等各种问题
除了 lightning attention 对 RL 训练的固有效率优势外,我们还提出了 CISPO,这是一种新颖的 RL 算法,进一步提高了 RL 效率。
CISPO 裁剪重要性采样权重而不是标记 token,优于其他 RL 变体。
结合 hybrid-attention 和 CISPO,MiniMaxM1 在 512 个 H800 GPU 上的完整 RL 训练仅需三周完成,租赁成本仅为 534,700 美元。
我们发布了两个版本的 MiniMax-M1 模型,分别具有 40K 和 80K 的 thinking budgets,其中 40K 模型代表 80K 训练的中间阶段。在复杂数学和编码任务上,MiniMax-M1-80k 优于 MiniMax-M1-40k
模型权重文件:https://github.com/MiniMax-AI/MiniMax-M1
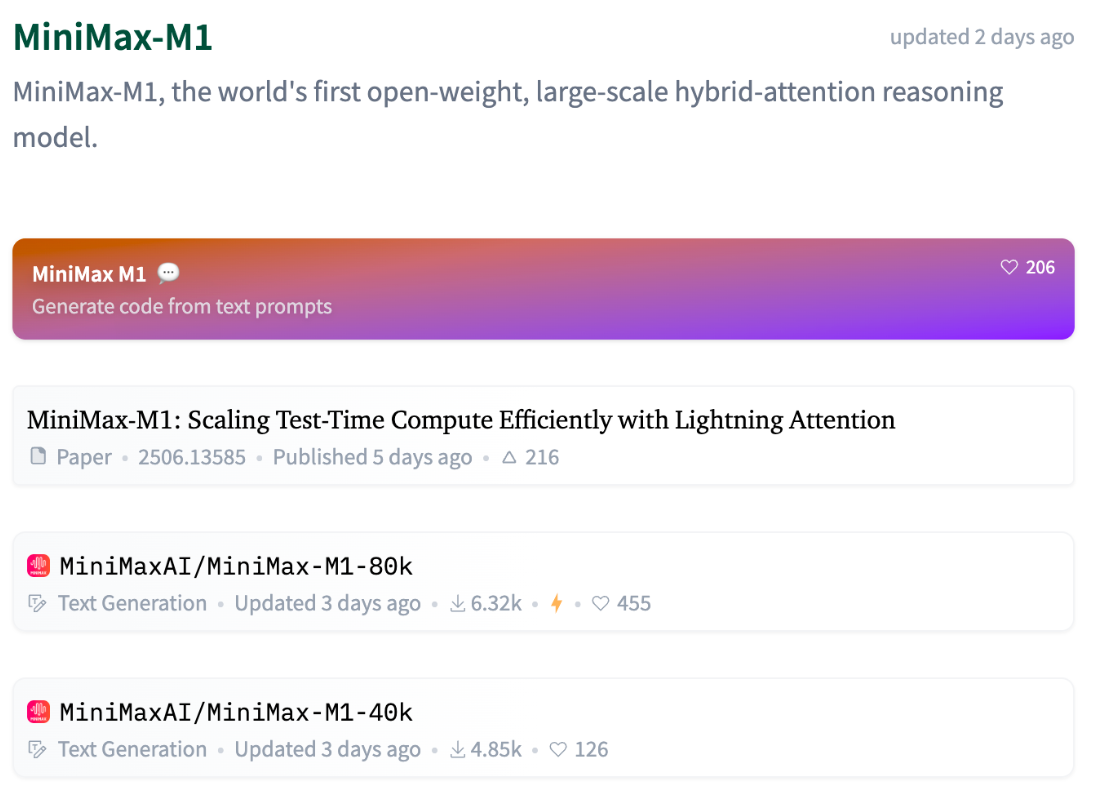
提取重点:hybrid attention、lightning attention、reasoning Model、RL、CISPO、MOE (456B-4.59B)、context length=100w tokens
对比 Deepseek-R1 MOE (671B-37B)、context length=128k,RL、GRPO
DeepSeek-V3-Base 作为基础模型,并采用 GRPO 作为 RL 框架,以提高 DeepSeek-R1-Zero 模型在推理方面的性能
DeepSeek-R1,它结合了少量冷启动数据和多阶段训练流程。具体来说,我们首先收集了数千个冷启动数据来微调 DeepSeek-V3-Base 模型。接下来,我们进行了与 DeepSeek-R1-Zero 类似的面向推理的 RL。当 RL 过程接近收敛时,我们通过在 RL 检查点上进行拒绝抽样,并结合来自 DeepSeek-V3 在写作、事实问答和自我认知等领域的监督数据,生成新的 SFT 数据,然后重新训练 DeepSeek-V3-Base 模型。
Deepseek-R1-zero 使用 GRPO
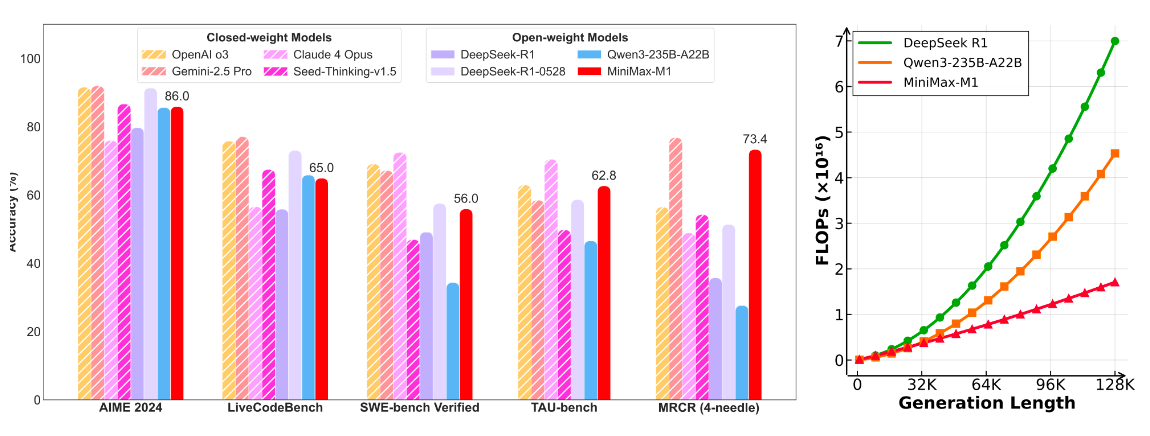
我们首先继续对 MiniMax-Text-01 进行预训练,使用精心挑选的、注重推理的语料库的 7.5 万亿个 tokens 上进行持续预训练。随后,我们进行监督微调(SFT),以注入特定的思维链(CoT)模式,为强化学习(这是 M1 开发的核心阶段)奠定坚实基础。
(1)我们提出了一种新颖的强化学习算法 CISPO,它摒弃了信任区域约束,转而对重要性采样权重进行裁剪,以稳定训练。这种方法在梯度计算中始终利用所有标记,与 GRPO 和 DAPO 相比,实证上实现了更高的效率。例如,在基于 Qwen2.5 - 32B 模型的受控研究中,CISPO 相较于 DAPO 实现了 2 倍的加速;
(2)尽管 M1 中的混合注意力设计自然地支持高效的强化学习扩展,但在使用这种架构进行强化学习扩展时,会出现独特的挑战。例如,我们发现架构的训练和推理内核之间存在精度不匹配问题,这会阻碍强化学习训练过程中的奖励增长。我们开发了针对性的解决方案来应对这些挑战,并成功地使用这种混合架构扩展强化学习。
# 训练过程
持续预训练 -> 冷启动 SFT -> RL
# 预训练
我们使用额外的 7.5 Ttokens (7.5 万亿 tokens),以优化的数据质量和数据混合方式,继续训练 MiniMax-Text-01 模型。
我们优先从各种来源(包括网页、论坛和教科书)中提取自然问题 - 答案(QA)对,同时严格避免使用合成数据。此外,我们对 QA 数据进行语义去重,以保持其多样性和独特性。此外,我们将 STEM(科学、技术、工程和数学)、代码、书籍和推理相关数据的比例提高到 70%。这显著增强了基础模型处理复杂任务的能力,同时不影响其其他一般能力。
我们降低了 MoE 辅助损失的系数,并调整了并行训练策略,以支持更大的训练 Micro batch size,这减轻了辅助损失对整体模型性能的负面影响。基于 MiniMax-Text-01,我们继续以 8e-5 的恒定学习率训练 2.5T 标记,然后在 5T 标记上衰减到 8e-6。
对于具有更高收敛复杂性的混合闪电架构模型,我们观察到过度激进的训练长度扩展可能导致训练过程中突然的梯度爆炸,对于闪电注意力,早期和后期层具有不同的衰减率,这使得早期层更多地关注局部信息。我们通过适应更平滑的上下文长度扩展来缓解这个问题,扩展过程分为四个阶段,从 32K 上下文窗口长度开始,最终将训练上下文扩展到 1M 标记。
关键词:7.5 万亿 tokens、学习率衰减,
# SFT
在持续预训练之后,我们进行监督微调(SFT),通过使用高质量示例来注入诸如基于反思的思维链(CoT)推理等期望行为,为下一阶段更高效、稳定的强化学习创建一个坚实的起点。具体而言,我们精心挑选具有长思维链响应的数据样本。这些数据样本涵盖数学、编程、STEM、写作、问答和多轮对话等不同领域。数学和编程样本约占所有数据的 60%。
# RL
在混合架构上扩展 RL 在过程中遇到了独特的挑战,为了解决这些困难,我们开发了有针对性的解决方案,使我们能够成功扩展 M1 的 RL 训练。此外,我们提出了一种新的 RL 算法,与现有方法相比,它实现了更高的 RL 效率。
# CISPO
对于来自数据集 D 的问题 q ,我们用 π 表示由 θ 参数化的策略模型,用 o 表示由策略生成的响应
回顾 PPO,GRPO
PPO:
其中 $$r_{i,t}(\theta)=\frac {\pi_{\theta}(o_{i,t}\vert q,o_{i,<t})}{\pi_{\theta_{\mathrm {old}}}(o_{i,t}\vert q,o_{i,<t})}$$ 是重要性采样(IS)权重,用于纠正在 off-policy 更新期间的分布
虽然近端策略优化算法(PPO)需要一个单独的价值模型来计算优势 $$\hatA}_{i,t}$$,但 GRPO 消除了价值模型,并将优势定义为相对于组内其他响应的输出奖励:$$ \hat {A}_{i,t} = \frac {R_i - \text {mean}(\{R_j\}_{j=1}\text{std}(\{R_j\}_{j=1} $$,其中 $$R_i$$ 是响应的奖励,G 个响应 $${o_i}\}_{i = 1}$$ 为每个问题采样
使用 zero-RL 设置对混合架构进行的初始实验中,我们观察到 GRPO 算法对训练性能产生了不利影响,我们最终确定了原始 PPO/GRPO 损失中不理想的裁剪操作是导致学习性能下降的主要因素。在策略更新期间,这些标记可能会表现出高 ri,t 值。结果,这些标记在第一次策略内更新后被裁剪掉,阻止了它们对后续策略外梯度更新的贡献。
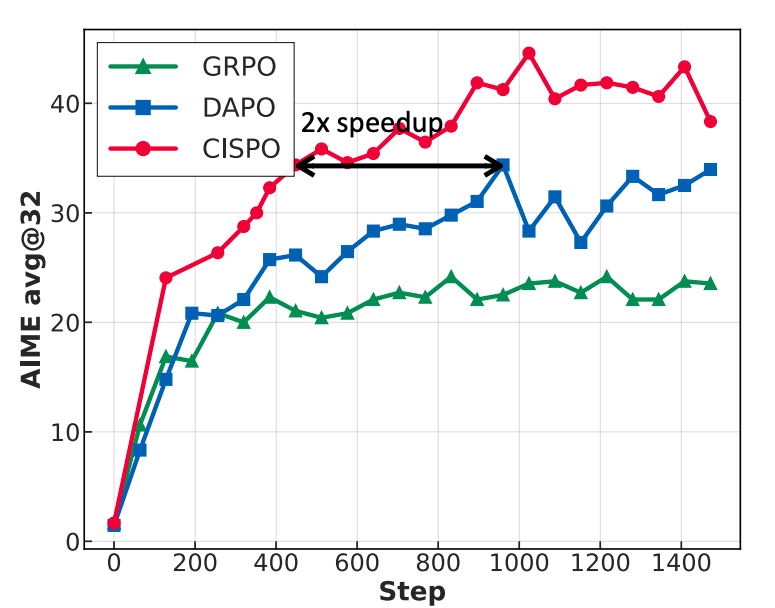
我们提出一种新算法,该算法明确避免丢弃 tokens,即使是那些与大幅更新相关的令牌,同时从本质上把熵维持在合理范围内,以确保稳定的探索。用于 offline 更新的具有校正分布的普通 REINFORCE objective 是:
其中 sg (・) 表示停止梯度操作。与 PPO/GRPO 中裁剪令牌更新不同,我们改为裁剪公式 reinforce 中的重要性采样权重,以稳定训练。我们将我们的方法称为 CISPO(裁剪重要性采样权重策略优化 - Clipped IS-weight Policy Optimization)。采用 GRPO 中的组相对优势和 token-level 损失,CISPO 优化以下目标:
\mathcal{J}_{\text{CISPO}}(\theta) = \mathbb{E}_{(q,a) \sim \mathcal{D}, \{o_i\}_{i=1}^G \sim \pi_{\theta_{\text{old}}}(\cdot \mid q)} \left[ \frac{1}{\sum_{i=1}^G |o_i|} \sum_{i=1}^G \sum_{t=1}^{|o_i|} \text{sg}(\hat{r}_{i,t}(\theta)) \hat{A}_{i,t} \log \pi_\theta(o_{i,t} \mid q, o_{i,相反,我们只调整了 $$\epsilon_high}$$。尽管由于权重裁剪,Jcispo 的梯度略有偏差,但这种方法保留了所有 tokens 的梯度贡献,特别是在长回复中。CISPO 在我们的实验中证明是有效的,有助于减少方差并稳定强化学习训练。此外,我们采用了动态采样和长度惩罚技术。CISPO 中没有 KL 惩罚项。
虽然我们在实验中采用了 CISPO,但在此我们通过在 CISPO 目标中引入逐个 tokens 的掩码,进一步给出一种统一的表述。这使得可以通过超参数调整来控制是否以及在何种条件下应舍弃来自特定 tokens 的梯度。unified formulation:
掩码 $$M_{i,t}$$ 等价于 PPO 信任区域中隐式定义的掩码,规则为: $$M_{i,t} = \begin {cases} 0 & \text {if } \hat {A}{i,t} > 0 \text{ and } r(\theta) > 1 + \epsilon_{\text{high}}, \ 0 & \text{if } \hat{A}{i,t} < 0 \text{ and } r(\theta) < 1 - \epsilon_{\text{low}}, \ 1 & \text{otherwise}. \end{cases}$$
这种统一的损失公式能够在一个通用框架下灵活地表示不同的裁剪策略。
CISPO 的实证验证。为了验证 CISPO 的有效性,我们在零强化学习训练设置下,将其与 DAPO 和 GRPO 进行实证比较。具体来说,我们应用不同的强化学习算法,在数学推理数据集上训练 Qwen2.5 - 32B - base 模型,并报告在 2024 年美国数学邀请赛(AIME)基准测试中的性能。如图 2 所示,在相同的训练步数下,CISPO 的性能显著优于 DAPO 和 GRPO。值得注意的是,与其他方法相比,CISPO 展现出卓越的训练效率;例如,它仅用 50% 的训练步数就达到了 DAPO 的性能。
关键词:CISPO、Clipped IS-weight (裁剪重要性采样权重) 、不对 IS 设下限、动态采样、长度惩罚、没有 KL 惩罚
# lightning attention
lightning attention 是线性注意力变体的 I/O aware 实现。
在我们的注意力设计中,每七个带有 lightning attention 的 transnormer 块后面跟着一个带有 softmax 注意力的 transformer 块。
这种设计理论上能够高效地将推理长度扩展到数十万个 tokens。不同推理模型支持的最大输入长度和输出长度(# tokens)

# lightning attention 扩展 RL
混合注意力本质上比传统注意力设计实现了更高效的 RL 扩展,因为展开计算和延迟通常是 RL 训练的主要瓶颈。然而,作为使用这种新颖架构进行大规模 RL 实验遇到了独特的挑战
生成和训练中的计算精度不匹配。RL 训练对计算精度高度敏感。在我们的 RL 训练中,我们观察到训练模式和推理模式下的生成 tokens 概率之间存在显著差异。通过逐层分析,我们确定输出层的 LM 头部的高强度激活是错误的主要来源。为了解决这个问题,我们将 LM 输出头部的精度提高到了 FP32。
优化器超参数敏感性。我们采用 AdamW 优化器,不适当的配置 β1, β2 和 ϵ 可能会导致训练期间不收敛。我们观察到 MiniMax-M1 训练中的梯度幅度范围很广,从 1e-18 到 1e-5,大多数梯度小于 1e-14。此外,相邻迭代的梯度之间的相关性很弱。基于此,我们设置 β1=0.9 , β2=0.95,和 eps=1e−15
通过重复检测进行早期截断。在强化学习训练过程中,我们发现复杂的提示可能会引发异常冗长且重复的回应,其巨大的梯度威胁到模型的稳定性。我们的目标是预先终止这些生成循环,而不是对已经重复的文本进行惩罚。由于简单的字符串匹配对于各种重复模式无效,我们开发了一种基于 tokens 概率的启发式方法。我们观察到,一旦模型进入重复循环,每个 tokens 的概率就会飙升。因此,我们实施了一个提前截断规则:如果连续 3000 个词元的概率都高于 0.99,则停止生成。这种方法通过消除这些冗余的长尾情况,成功地防止了模型不稳定,并提高了生成吞吐量。
# 将强化学习扩展应用于更长的思考过程
首次强化学习训练在输出长度限制为 40Ktokens 的情况下进行。鉴于 M1 的混合架构天生支持更长序列的近似线性缩放,我们在强化学习训练期间将生成长度进一步扩展到 80Ktokens。这产生了一个新模型,我们将其称为 MiniMax-M1-80k。
为了有效地训练我们的 RL 模型以 80K 输出长度,我们利用我们之前训练的 40K 模型来指导数据过滤过程。
为了逐渐增加输出长度,我们采用分阶段的窗口扩展 RL 策略。我们从 40K 的输出长度开始,逐步扩展到 48K、56K、64K、72K,最终达到 80K。这种分阶段的方法确保了每一步的训练稳定性。过渡到下一个长度是由一组经验指标决定的。
解决训练不稳定问题。具体而言,该模型表现出对模式崩溃的敏感性,即生成序列的后半部分会退化为不连贯或混乱的文本。跟因为:在输出长度扩展过程中,负样本长度的增长速度比正样本快得多,常常更早达到上下文窗口限制。因此,在生成序列的后半段会积累不成比例的大的负梯度。这种不平衡源于 GRPO 的优势归一化本质上的不平等特性以及我们采用的 token-level loss。为解决这一问题,我们实施三个关键解决方案:(1) 检测重复模式(连续的高概率词元)并提前停止,以防止重复回复过度消耗上下文窗口;(2) 采用 sample-level loss 和 token-level normalization 相结合的方式,缓解正负样本不平衡问题并减轻不良影响;(3) 同时降低梯度裁剪阈值和 $$\epsilon^{IS}_{high}$$ 以进一步稳定奖励。
# 结论
我们介绍并发布 MiniMax-M1,这是世界上第一个采用 lightning attention 的开放权重、大规模推理模型。这种高效的注意力设计使 MiniMax-M1 能够原生支持高达 1M 个标记的输入和 80K 个标记的生成长度 —— 这两者都显著超过了其他开放权重模型的能力。这些特性使 MiniMax-M1 特别适合需要长上下文和扩展推理的复杂、现实场景,这些特性通过其在软件工程、Agent 工具使用和长上下文理解基准测试中的强劲表现得到了实证验证。除了闪电注意力对 RL 训练固有的效率优势之外,这项工作还贡献了一种新颖的 RL 算法 CISPO,以加速训练。结合架构优势与 CISPO,我们高效地训练了 MiniMax-M1,完整的 RL 训练在 512 个 H800 GPU 上完成,仅需三周。在全面的评估中, MiniMax-M1 与 DeepSeek-R1 和 Qwen3-235B 并列为世界上最优秀的开放权重模型。
展望未来,随着测试时的计算能力不断提升,以支持日益复杂的场景,我们预见到这种高效架构在应对现实世界挑战方面具有巨大潜力。这些挑战包括公司工作流程自动化和开展科学研究。现实世界的应用尤其需要语言推理模型(LRM)作为与环境、工具、计算机或其他智能体交互的智能体发挥作用,这需要在几十到几百个回合中进行推理,同时整合来自不同来源的长上下文信息。我们设想 MiniMax - M1 凭借独特优势,为这类应用提供坚实基础,并且我们将全力以赴朝着这一目标进一步发展 MiniMax - M1。
# Deepseek-R1
# introduction
DeepSeek-R1-Zero 是一个通过大规模强化学习(RL)训练的模型,没有使用监督微调(SFT)作为初步步骤。DeepSeek-R1,它在强化学习之前加入了多阶段训练和冷启动数据。
DeepSeek-R1-Zero 使用 DeepSeek-V3-Base 作为基础模型,并采用 GRPO 作为强化学习框架,以提高模型在推理中的表现。在训练过程中,DeepSeek-R1-Zero 自然涌现出许多强大且有趣的推理行为。经过数千次强化学习步骤后,DeepSeek-R1-Zero 在推理基准测试中表现出色。
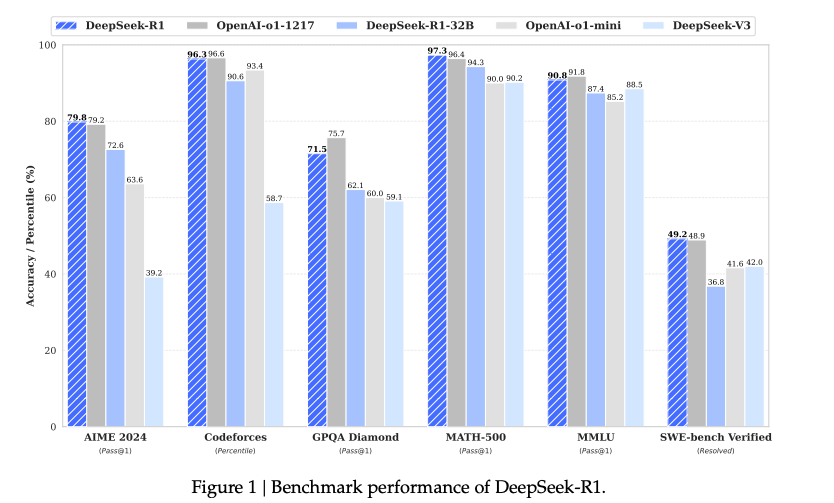
DeepSeek-R1-Zero 也面临一些挑战,如可读性差和语言混合问题。为了解决这些问题并进一步提升推理性能,我们引入了 DeepSeek-R1,它结合了少量冷启动数据和多阶段训练流程。
我们首先收集数千条冷启动数据来微调 DeepSeek-V3-Base 模型。随后,我们像 DeepSeek-R1-Zero 一样进行面向推理的强化学习。在强化学习过程接近收敛时,我们通过对强化学习检查点进行拒绝采样来创建新的监督微调数据,并结合来自 DeepSeek-V3 的写作、事实问答和自我认知等领域的监督数据,然后重新训练 DeepSeek-V3-Base 模型。在使用新数据进行微调后,检查点会经历额外的强化学习过程,考虑所有场景的提示。经过这些步骤后,我们得到了一个称为 DeepSeek-R1 的检查点
# Method
1、GRPO
2、奖励模型
奖励是训练信号的来源,决定了强化学习的优化方向。为了训练 DeepSeek-R1-Zero,我们采用了一个基于规则的奖励系统,主要包括两种类型的奖励:
- 准确性奖励:准确性奖励模型评估响应是否正确。
- 格式奖励:除了准确性奖励模型外,我们还使用了一个格式奖励模型,强制模型将其思维过程放在
<think>和</think>标签之间。
3、带冷启动的强化学习
我们为 DeepSeek-R1 构建并收集了少量长思维链(CoT)数据,以微调模型作为初始的强化学习 Actor。我们收集了数千条冷启动数据来微调 DeepSeek-V3-Base,作为强化学习的起点。我们设计了一种可读的模式,包括每个响应末尾的摘要,并过滤掉不便于阅读的响应。我们定义输出格式为 |special_token|<reasoning_process>|special_token|<summary>
为了缓解语言混合问题,我们在强化学习训练中引入了语言一致性奖励,该奖励根据思维链中目标语言单词的比例计算。尽管消融实验表明这种对齐会导致模型性能略有下降,但这种奖励符合人类偏好,使其更具可读性。。最后,我们将推理任务的准确性和语言一致性奖励直接相加,形成最终奖励。然后,我们在微调后的模型上进行强化学习训练,直到其在推理任务上达到收敛。
我们利用得到的检查点来收集用于后续轮次的 SFT(监督微调)数据。与最初主要关注推理的冷启动数据不同,此阶段纳入了来自其他领域的数据,以提升模型在写作、角色扮演和其他通用任务方面的能力。具体而言,我们按如下所述生成数据并微调模型。
- 推理数据 我们精心整理推理提示,并通过从上述强化学习训练的检查点进行拒绝采样来生成推理轨迹。在前一阶段,我们只纳入了可以使用基于规则的奖励进行评估的数据。然而,在这个阶段,我们通过纳入更多数据来扩展数据集,其中一些数据使用生成式奖励模型,将真实情况和模型预测输入到 DeepSeek-V3 中进行判断。此外,由于模型输出有时杂乱且难以阅读,我们过滤掉了包含混合语言、长篇段落和代码块的思维链。对于每个提示,我们采样多个回复,只保留正确的回复。总体而言,我们收集了约 60 万个与推理相关的训练样本。
- 对于非推理数据,如写作、事实性问答、自我认知和翻译等,我们采用 DeepSeek-V3 流程,并复用 DeepSeek-V3 的部分监督微调(SFT)数据集。对于某些非推理任务,我们会调用 DeepSeek-V3 在通过提示回答问题之前生成一个潜在的思维链。然而,对于更简单的查询,如 “hello”,我们不会在回复中提供思维链。最终,我们总共收集了大约 20 万个与推理无关的训练样本。
- 我们使用上述约 80 万条样本对 DeepSeek-V3-Base 进行了两个 epochs 的微调。
为了进一步使模型与人类偏好对齐,我们实施了第二个强化学习阶段,旨在提高模型的有用性和无害性,同时优化其推理能力。具体来说,我们使用奖励信号和多样化的提示分布来训练模型。对于推理数据,我们遵循 DeepSeek-R1-Zero 的方法,使用基于规则的奖励来指导数学、代码和逻辑推理领域的学习过程。
# veRL
# single controller 和 multi controller
在一个复杂的工作流程中,single controller 只有一个程序负责管理,而其他的子模块只负责执行。所有控制逻辑都写在唯一 controller 上,实现简单,便于调试。然而,single controller 所承担的控制压力巨大,一来,通讯强度大而效率堪忧,二来,倘若 single controller 崩溃,整个系统将彻底失效。反过来,multi controller 则有多个控制程序来管理不同的子模块,每个子模块仍旧只负责执行自己的功能。如此以来,单个控制程序的管理压力降低,系统更加鲁棒可扩展。然而,控制逻辑分散在多个程序中,实现复杂,难以调试。
大型语言模型 RL 本质上是一个二维的 DataFlow 问题:高级控制流 (描述 RL 算法的流程)+ 低级计算流 (描述分布式神经网络计算)。
actor 在 RLHF 会进行 auto-regressive decoding,而 critic, reward 和 reference 则只会 prefill,不会 decode。所以,我们将 actor 的推理特定称为 rollout,而其他模型的推理称为 inference。
multi-contoller 能够有效的降低通讯压力,提升系统鲁棒性。然而,如果最顶层的 controller 也是 multi-controller 的,其实对用户会非常复杂。在一个 controller 内代码的修改,需要将所有 dependency 都修改一遍。
veRL 在上层暴露出 single controller 的接口,并进行完善的封装。用户能够基于算法设计,自由组合并行策略(3D 并行、ZeRO 还有 FSDP),直接对子模块进行拼装;而在每个子模块内部,采用 multi-controller,提供强劲的效率。当然,可能更改子模块就会相对麻烦。控制流由具有全局视图的单控制器 (Single-Controller) 管理,从而能够简单高效地实现新的控制流。计算流则由多控制器 (Multi-Controller) 处理,确保计算的高效执行,并可在不同的控制流中复用。
# hybrid engine
在 RLHF 流程中,actor model 的 generation 和 rollout 占据了绝大多数运行时间(在 veRL 是 58.9%)。并且,由于 PPO 是 on-policy 算法,经验(experiences)必须来自于被 train 的模型本身,因此,rollout 和 training 是必须串行的。如果这两者使用不同的资源组,比如 rollout 用 2 张卡,而 training 用 4 张卡,rollout 的时候 training 的资源闲置,training 的时候 rollout 的资源闲置,无论如何都会浪费大量的计算资源。由此,veRL 将 training 和 rollout engine 放置在同一个资源组中串行执行。training 时,将 rollout engine 的显存回收(offload 到 CPU 上 或者直接析构掉),rollout 时,再将 training engine 的显存释放掉。这种将 actor model 的不同 engine 放置在同一个资源组上的方案,就称为 hybrid engine。
actor model 需要 training engine 和 rollout engine。前者是用现代 training engine,比如 Megatron 或者 FSDP,后者得用现代推理引擎,比如 SGLang 或者 vllm 作为 rollout engine。
除开 hybrid engine 之外,类似共用资源组的方法还有 collocate。
# 强化学习数学解释
# 马尔可夫决策过程(MDP)
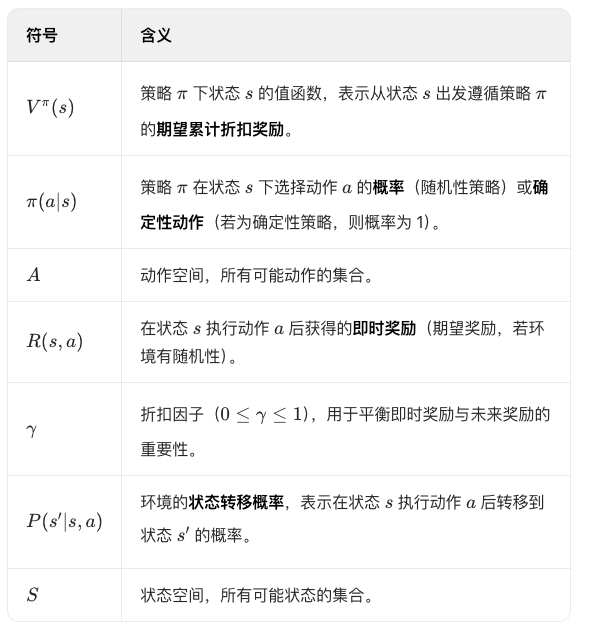
马尔可夫决策过程(Markov Decision Process,MDP)是强化学习的数学基础,它为序列决策问题提供了一个形式化的框架。MDP 由以下五个核心元素组成:
- 状态集合 S:描述环境可能处于的所有状态。
- 动作集合 A:描述智能体在每个状态下可以执行的所有动作。
- 转移概率函数 $$P (s’|s,a)$$:描述在状态 s 下执行动作 a 后,环境转移到状态 s’的概率。
- 奖励函数 $$ R (s,a,s’)$$:描述在状态 s 下执行动作 a 并转移到状态 s’时获得的即时奖励。
- 折扣因子 γ:介于 0 和 1 之间的值,用于平衡即时奖励和未来奖励的重要性。
马尔可夫决策过程的一个重要性质是:下一个时刻的状态只取决于当前状态,而不会受到过去状态的影响,即状态转移概率:
下一个时刻的状态 $$S_{t+1}$$ 取决于当前的动作 $$A_t$$ 和当前状态 $$S_t$$
# 价值函数
在强化学习中,策略(Policy)定义了智能体在给定状态下应该采取的行动。策略可以是确定性的,即对每个状态确定一个动作,表示为 $$π(s) = a$$;也可以是随机的,即对每个状态定义一个动作的概率分布,表示为 $$ π(a|s)$$。
- 状态价值函数 $$V^π(s)$$:在策略 π 下,从状态 s 开始的期望累积折扣奖励:
- (V^{\pi}(s)$$:表示在策略 $$\pi$$下,状态 s 的值函数(Value Function),即从状态 s 出发,遵循策略$$\pi$$所能获得的期望累计奖励。
- \sum_{k=0}^{\infty} \gamma^k R_{t+k+1}$$:表示从当前时刻 t 开始,未来所有奖励的折扣累计和(Discounted Cumulative Reward)。
- V^{\pi}(s)$$表示你按照策略$$\pi$$玩下去,从当前关卡开始能获得的期望总分(考虑了未来所有可能的操作和关卡变化,且越往后的分数权重越低)。
- 动作价值函数 $$Q^π(s,a)$$:在策略 π 下,在状态 s 执行动作 a 后的期望累积折扣奖励:
- Q^{\pi}(s, a)$$:表示在策略 π 下,状态 s 执行动作 a 的动作值函数(也称 Q 函数),即从状态 s 出发,先执行动作 a,然后遵循策略π 所能获得的期望累计折扣奖励。
- \sum_{k=0}^{\infty} \gamma^k R_{t+k+1}$$:与值函数$$ V^{\pi}(s)$$ 类似 ,仍是未来所有奖励的折扣累计和,但起点是执行动作 a 后的下一时刻。
- Q^{\pi}(s, a)$$表示你选择动作 a 后,按照策略 $$\pi$$(如 “优先保命还是进攻”)玩下去的期望总分。
- 核心思想:Q 函数将 “状态” 和 “动作” 直接关联,提供了一种动作评价机制,使智能体可以通过比较不同动作的 Q 值来选择最优行为。这是许多强化学习算法(如 Q-Learning、Sarsa)的核心。
这两个价值函数之间存在以下关系:
状态 s 的价值等于策略 $$\pi$$ 下所有可能动作的 Q 值的加权平均(权重为动作选择概率 $$\pi (a|s)$$。
假设你在玩一个游戏,当前状态 s 有两种可选动作:
- 动作 $$a_1$$(概率 $$ \pi (a_1|s) = 0.7$$:Q 值 $$Q^{\pi}(s, a_1) = 100$$;
- 动作 $$a_2$$(概率 $$ \pi (a_2|s) = 0.3$$:Q 值 $$Q^{\pi}(s, a_2) = 50$$。
则状态 s 的价值为:$$V^{\pi}(s) = 0.7 \times 100 + 0.3 \times 50 = 85$$
状态的价值取决于在该状态下可采取的动作及其后续结果。通过动作值函数的加权平均,状态值函数隐式包含了策略的决策逻辑。
# 贝尔曼方程
贝尔曼方程(Bellman Equations)是强化学习中的基本方程,它描述了价值函数的递归关系。对于状态价值函数和动作价值函数,贝尔曼方程分别为:
贝尔曼期望方程(针对给定策略 π):
- 即时奖励项:$$R (s,a)$$ 是执行动作 $$a$$ 后立即获得的奖励,体现了当前决策的直接收益。
- 未来奖励项:$$\gamma \sum_s’ \in S} P(s’|s,a) V(s’)$$ 是后续状态价值的加权平均,其中:
- \gamma$$是折扣因子,用于衰减未来奖励的价值(越远的奖励影响越小);
公式中 $$V^{\pi}(s’)$$ 是下一状态 s’的值函数,这表明 当前状态的价值依赖于未来状态的价值,形成了一个递归结构。
假设你在棋盘状态 s 上,策略 $$\pi$$ 告诉你:
- 有 70% 的概率走棋 $$a_1$$,即时奖励 $$R (s,a_1)=1$$,且有 50% 概率转移到状态 $$s_1$$$$(V^\pi}(s_1’)=1$$,50% 概率转移到状态 $$s_2$$ $$(V(s_2’)=5$$;
- 有 30% 的概率走棋 $$a_2$$,即时奖励 $$R (s,a_2)=$$0,且必定转移到状态 $$s_3$$ $$(V^{\pi}(s_3’)=8$$。
则状态 s 的价值为:
\begin{align} V^{\pi}(s) &= 0.7 \times \left[ 1 + \gamma \left( 0.5 \times 10 + 0.5 \times 5 \right) \right] + 0.3 \times \left[ 0 + \gamma \times 8 \right] \\ &= 0.7 \times (1 + 7.5\gamma) + 0.3 \times 8\gamma \\ &= 0.7 + 5.25\gamma + 2.4\gamma \\ &= 0.7 + 7.65\gamma \end{align}
- 若 $$gamma=1$$(不折扣未来奖励),则 $$V^{\pi}(s)=8.35$$,体现了对所有可能动作和后续状态的综合评估。
Q^\pi(s,a)$$未来累计折扣奖励的期望值。 它由两部分组成: 1. 即时奖励 $$R(s,a)$$:执行动作 a 后立即获得的奖励。 2. 未来奖励的期望值:执行动作 a 后转移到所有可能的下一状态 s',并在每个 s' 下根据策略 $$\pi$$选择动作 a'所带来的后续价值,需考虑折扣因子 $$\gamma$$和状态转移概率$$ P(s'|s,a)$$。 $$R(s,a) + \gamma \sum_{s' \in S} P(s'|s,a) \underbrace{\sum_{a' \in A} \pi(a'|s') Q^{\pi}(s',a')}_{\text{下一状态 } s' \text{ 的价值期望}}
- 第一步:执行动作 a 后,环境以概率 $$P (s’|s,a$$ 转移到下一状态 s’ 。
- 第二步:在状态 s’ 时,策略 $$\pi$$ 以概率 $$\pi (a’|s’) $$ 选择动作 a’ ,此时 $$ Q^\pi (s’,a’) $$ 表示从 $$(s’,a’)$$ 开始的未来累计折扣奖励期望。
- 第三步:对所有可能的 s’ 和 a’ 求期望(即双重求和),并通过 $$\gamma$$ 折扣化,得到当前动作 a 带来的未来奖励总期望。
贝尔曼最优方程(针对最优策略):
强化学习的目标是找到一个策略 $$πθ(a|s)$$ ,使得智能体在与环境交互的过程中能够最大化期望累积奖励。假设策略 $$πθ$$ 是由参数 θ 参数化的,那么目标可以表示为:
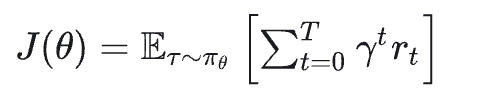
其中:
- τ=(s0,a0,s1,a1,...)$$ 是一个轨迹(Trajectory),表示智能体与环境交互的序列。
- r_t$$ 是在时间步 t 获得的奖励。
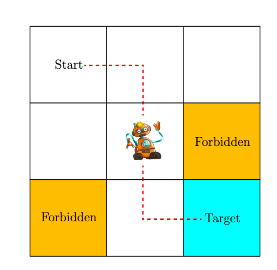
state
State space: $$S={S_i}^9_{i=1}$$
Action
Action space of a state : $$A(s_i)={a_i}^5_{i=1}$$
state transition: $$s1 ->a2 -> s2$$
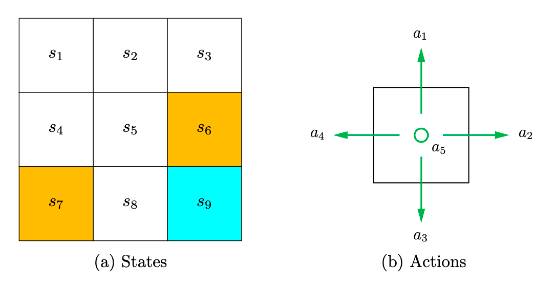
state transition probability:$$p (s2|s1,a2)=1 \p (si|s1,a2)=0,i {=}\mathllap {/,} 2$$ 在 State s1,选择 action a2,下一个状态是 s2
policy:在当前状态采取的行动。基于策略可以得到 paths
policy 数学描述:对于状态 s1,$$\pi (a1|s1)=0$$, 在状态 s1 下,选择 a1 action 的概率是 0。所有概率和 = 1
reward:agent 采取动作后会得到的一个标量。正数数鼓励的,负数惩罚。
reward 数学表示: $$p (r=-1|s1,a1)=1 \ p (r {=}\mathllap {/,}-1|s1,a1)=0$$ 在 s1,采取 a1 策略,得到 - 1 奖励的概率为 1。reward 依赖当前 state 和 action
trajectory: state-action-reward chain
return : 沿着 trajectory 相加所有 reward
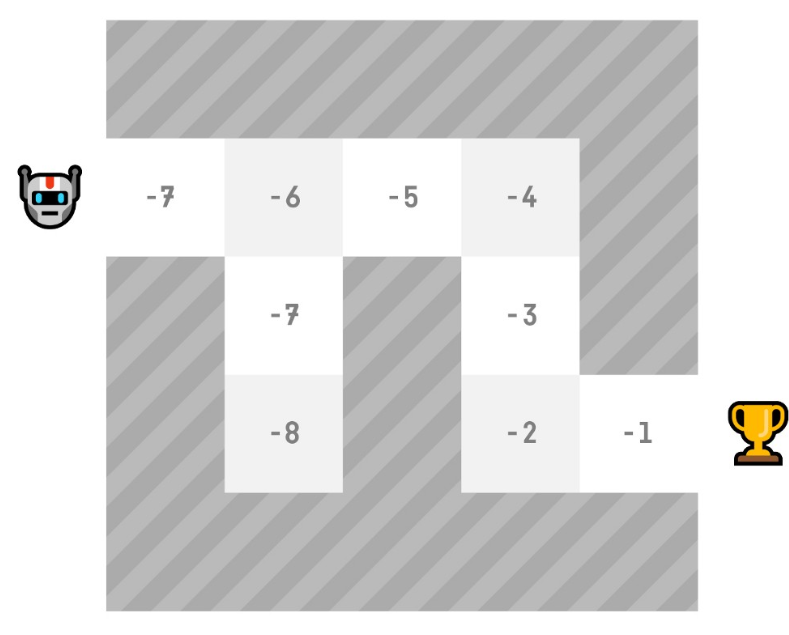
discounted return : discount rare $$\gamma [0,1)$$, $$discount _return :\fracr$$。
If $$\gamma$$ is close to 0, the value of the discounted return is dominated by the rewards obtained in the near future.
If $$\gamma$$ is close to 1, the value of the discounted return is dominated by the rewards obtained in the far future.
episode:terminal state
# MDP - markov decision process
图中的公式为:
markov process
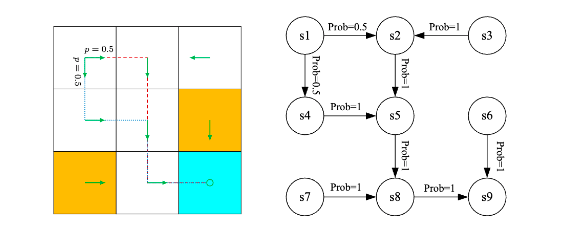
# 2、bellman equation
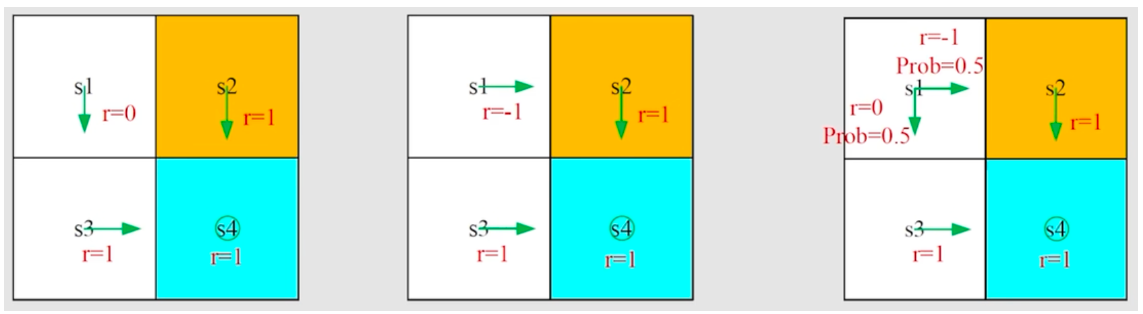
v1 定义 从 si 出发得到的 return
\begin{align} v_1 &= r_1 + \gamma(r_2 + \gamma r_3 + \dots) = r_1 + \gamma v_2\\ v_2 &= r_2 + \gamma(r_3 + \gamma r_4 + \dots) = r_2 + \gamma v_3\\ v_3 &= r_3 + \gamma(r_4 + \gamma r_1 + \dots) = r_3 + \gamma v_4\\ v_4 &= r_4 + \gamma(r_1 + \gamma r_2 + \dots) = r_4 + \gamma v_1 \end{align}bootstrapping : returns 依赖以其他状态 value
discounted return:
state value: Gt 的期望值
基于 policy $$\pi $$,不同策略,state value 不同
state value 是多个 trajectory 的平均值
bellman equation 描述不同状态的 state value
\begin{align} v_{\pi}(s) &= \mathbb{E}[R_{t + 1} \mid S_t = s] + \gamma\mathbb{E}[G_{t + 1} \mid S_t = s] \\ &= \underbrace{\sum_{a} \pi(a \mid s) \sum_{r} p(r \mid s, a)r}_{\text{mean of immediate rewards}} + \gamma\underbrace{\sum_{a} \pi(a \mid s) \sum_{s'} p(s' \mid s, a)v_{\pi}(s')}_{\text{mean of future rewards}} \\ &= \sum_{a} \pi(a \mid s) \left[ \sum_{r} p(r \mid s, a)r + \gamma \sum_{s'} p(s' \mid s, a)v_{\pi}(s') \right], \quad \forall s \in \mathcal{S} \end{align}
其中:
# matrix-vector form
四个 states 时,
# solve state value
用于评估策略,可以找到更好的策略
一种迭代的方案:
V_{k+1}=r_{\pi}+\gamma P_{\pi}V_{k}$$ ,可以证明,$$v_k->v_{\pi}# action value
从一个 state 出发,进行一个 action 之后得到的 return
# 3、bellman optimality equation
A policy $$\pi*$$ is optimal if $$v_\pi(s) \geq v_{\pi}(s)$$ for all s and for any other policy$$\pi$$.
v(s),v(s'),\pi(a|s)$$ 是未知的 ##### matrix-vector form $$v=\max_{\pi}(r_{\pi}+\gamma P_{\pi}v)
# 4、值迭代 / 策略迭代
# 值迭代
从 $$V_0$$ 触发
1、策略更新
2、值更新
# 策略迭代
从 $$\pi_0$$ 触发
1、策略评估:计算 $$\pi_k$$ 的 state value
2、策略优化
# truncated
# 5、monte carlo estimation
基本思想:model free
# soft policy
\varepsilon$$-greedy $$ \pi(a \mid s)= \begin{cases} 1 - \frac{\varepsilon}{|\mathcal{A}(s)|}(|\mathcal{A}(s)| - 1), & \text{for the greedy action}, \\ \frac{\varepsilon}{|\mathcal{A}(s)|}, & \text{for the other } |\mathcal{A}(s)| - 1 \text{ actions}. \end{cases}where $$ \varepsilon \in [0, 1] $$and$$|\mathcal{A}(s)|$$ is the number of actions for s.
MC-Based
where $$\Pi_{\varepsilon} $$denotes the set of all$$ \varepsilon$$ - greedy policies with a fixed value of $$ \varepsilon$$. The optimal policy here is
\epsilon$$比较大时探索性比较强 #### 6、Stochastic approximation ##### Robbins-Monro goal: $$g(w)=0 W_{k+1}=W_k-a_k\tilde{g}(W_k,\eta_k)$$,$$\tilde{g}(W_k,\eta_k)=g(w_k)+\eta_k
# SGD
goal: $$\min_w J(W)=\mathbb{E}[f(w,X)]$$
method1: GD : $$ w_{k + 1} = w_k - \alpha_k \nabla_w \mathbb{E}[f(w_k, X)] = w_k - \alpha_k \mathbb{E}[\nabla_w f(w_k, X)] $$
method2: BGD $$ \mathbbE}[\nabla_w f(w_k, X)] \approx \frac{1}{n} \sum_{i = 1} \nabla_w f(w_k, x_i) \ w_k + 1} = w_k - \alpha_k \frac{1}{n} \sum_{i = 1} \nabla_w f(w_k, x_i) $$
method3: SGD $$ w_{k + 1} = w_k - \alpha_k \nabla_w f(w_k, x_k) $$
# 7、TD
一种 model-free 的方法